ベイジアンモデリングを使用することのメリットの一つとして、分析者の知見をモデルに反映させやすいという点があります。
例えば、
$$ y = \alpha + \beta X +\varepsilon$$
という単回帰を考える際、「変数$X$が1増えたときに、$y$に与える影響は大体0.5くらいだろう」という知見があるのであれば、回帰係数$\beta$の事前分布の平均を0.5に設定する、などのアプローチをとることができます。
しかし、ベイジアンニューラルネットワーク(以下、BNNと記載します)を使用する場合には、一般的には知見を事前分布という形でモデルに反映させることは難しいです。なぜなら、重み$w$と目的変数$y$の間に複雑な関係式が存在しており、$w$が$y$に与える影響が自明ではないためです。
そのため、BNNの重み$w$の事前分布には、とりあえず平均に0、共分散行列に$\sigma^2 I$の多変量正規分布を使用することが多いようです。(Isotropic Gaussian Priorと呼ぶらしい)
と思っていたら、『Bayesian Neural Networks with Domain Knowledge Priors』という論文にて、事前分布に知見を反映させる方法が提案されていました。
今回はその方法をご紹介するとともに、Pyroを使った実装も併せてご紹介します。
重みの事前分布にドメイン知識を反映させる方法
まず、各種記号を定義します。特徴量$X$の空間を$\mathcal{X}$、目的変数$y$の空間を$\mathcal{Y}$とします。また、ニューラルネットワークのクラス$\mathcal{H}$を以下のように定義します。(ただし、$w$はニューラルネットワークの重みを表します)
$$
\mathcal{H} = \{h_w | h_w: \mathcal{X} \rightarrow \mathcal{Y} \}
$$
ドメイン損失関数の定義
このような設定のもと、さらにドメイン知識損失関数$\phi$というものを分析者が独自に定義します。この$\phi$は、
$$
\phi : \mathcal{H} \times \mathcal{X} \rightarrow \mathbb{R}
$$
であり、かつ$\phi(h_w, x) \geq 0$を満たすようにします。さらに、点$x$における$h_w(x)$の値がドメイン知識に従っているほど、$\phi(h_w, x)$の値が0に近くなるように設計します。
$\phi$が上記性質を満たすとき、データ$X$および重みパラメータ$w$が与えられた場合の尤度$p(\phi|w, X)$を、以下のように平均0、分散$\tau^2$の正規分布に設定します。($\tau^2$はハイパーパラメータ)
$$
p(\phi| w, X) = \prod_{x\in X}\mathcal{N} (\phi(h_w, x); 0, \tau^2)
$$
このように設定することで、
- $h_w(x)$の値がドメイン知識に近いほど、$\phi(h_w, x)$の値が0に近くなり、尤度は大きくなる
- $\tau^2$の値を小さくするほど、ドメイン知識に近いときと遠いときの尤度値の差が大きくなる
ということがわかります。
尤度を上記のように設定すると、$w$の事後分布は以下のようになります。
$$
p(w | \phi, X) \propto p(\phi | X, w) p(w) = \prod_{x\in X}\mathcal{N} (\phi(h_w, x); 0, \tau^2) \cdot p(w)
$$
$p(w)$は$w$の事前分布で、先述のIsotropic Gaussian Priorを使います。
$$
p(w) = \prod_i N(w; 0, \sigma^2)
$$
この事後分布$p(w | \phi, X)$は解析的に導出することはできないので、変分推論で近似した事後分布を求めることになります。
(余談ですが、$\phi(h_w, x)$は非負の値しかとらないので、$\mathcal{N} (\phi(h_w, x); 0, \tau^2)$は実質的には半正規分布になります。であれば、別に尤度は正規分布でなくても、指数分布やガンマ分布など、サポートが非負の確率分布を最初から使えばいいんじゃない?と個人的に思いました。)
学習ステップ
$\phi$が設計できたら、以下のステップでニューラルネットワークの学習を行います。
- 【事前学習】データ$X^\prime$を用い、$\phi$が小さくなるよう、重み$w$の事前分布を学習する
- 【本学習】データ$X$と$y$を用い、BNNの予測値と実測値との乖離が小さくなるよう、重み$w$の事後分布を計算する
ここでデータ$X^\prime$はunlabeld data(=目的変数の値が分かっていないデータ)であり、データ$X$と同じである必要はありません。
著者らはこの提案手法を“Banana”と呼んでいます。が、”Banana”という名称の由来については特に述べられていませんでした。(なんでや。。。)
下図の下段が、このBananaで行っている処理のイメージです。1段階目に事前学習させた事前分布(=Informative Prior)を導出し、2段階目に本番のモデルを構築し、事後分布を導出します。
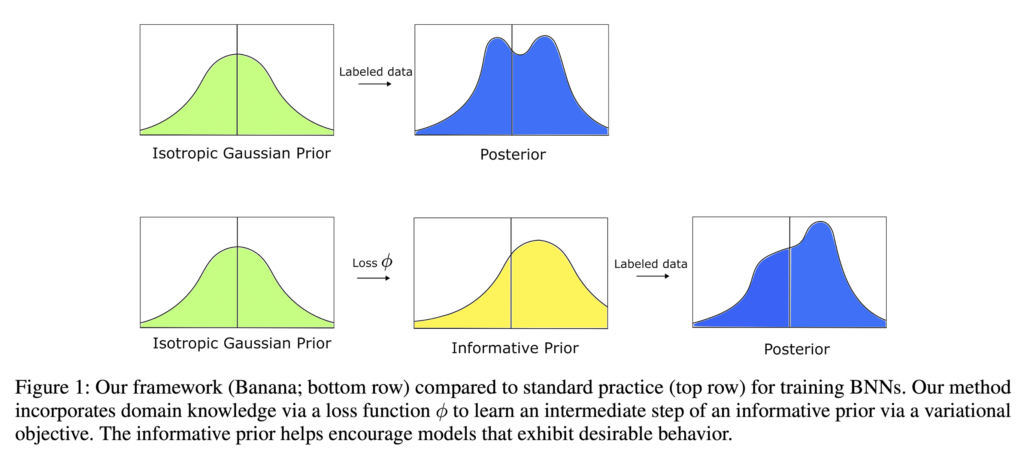
ただ、データ$X^\prime$は$X$と同じである必要はないのですが、特にunlabeld dataが存在しない場合、つまり手元にあるデータ全ての目的変数の値が得られている場合に、
- $X$と$X^\prime$は全く同じ($X=X^\prime$)であっても問題ないのか
- データの一部を$X^\prime$として切り出し、残りを$X^\prime$として扱うべきなのか
というのが気になりました。
前者の場合は、データ$X$をステップ1と2の両方で使用することになります。後者の場合は、全てのデータ$X_{all}$を$X$と$X^\prime$に分割し、$X^\prime$をステップ1に、$X$をステップ2に使用することになります。
論文中には、この辺の細かい取り扱いについては特に明記されていないようでした。特に$X$と$X^\prime$を分けるメリットもないかなと思うので、本記事では、前者の方法(=ステップ1でも2でも同じ$X$を用いる)をとることにします。
Decoy MNISTを用いた実装例
論文では、このbananaという手法を、Decoy MNISTという画像データを使った画像分類モデルに適用した例が載っていましたので、この記事ではそれを実際にPythonおよびPyroで実装してみようと思います。
(注:ハイパーパラメータ等の細かい設定は、論文とは異なりますのでご了承ください)
Decoy MNISTとは?
Decoy MNISTはこちらの論文で使用されている画像データセットで、MNISTに以下の処理をかますことで、意図的に分布シフト(=trainデータとtestデータ間でデータの分布が異なる現象)を発生させています。
- 各画像の4隅からランダムに4×4のセルを1つ選択
- 1で選ばれた4×4セルに対し、以下の処理を実行
- trainデータ:セルの値を$255 − 25y$に上書き ($y$は数値ラベル)
- testデータ:セルの値を0~255の間からランダムに選択し上書き
Pythonで実際にDecoy MNISTを作成してみます。
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt
import random
from tqdm import tqdm
# MNISTデータ読み込みには、『ゼロから作るDeep Learning』のコードを流用
# https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/dataset/mnist.py
from mnist import load_mnist
torch.set_default_device("cuda")
N_train = 60000
N_test = 10000
# MNISTデータ読み込み
train, test = load_mnist(normalize=True, flatten=False, one_hot_label=False)
X_train = np.squeeze(train[0])[:N_train]
y_train = train[1][:N_train]
X_test = np.squeeze(test[0][:N_test])
y_test = test[1][:N_test]
# decoy処理を実行する関数を定義
def create_decoy_mnist(images, labels=None, seed=123):
"""MNISTデータにdecoy処理をかける"""
# シード固定
random.seed(seed)
# 画像データのコピーを作成
decoy_images = images.copy()
# 各画像に対して処理を適用
for n, image in enumerate(decoy_images):
# 4つの隅からランダムにひとつ選択
corner_start = random.choice(
[[0, 0], [0, 24], [24, 0], [24, 24]] # 左上, 左下, 右上, 右下
)
corner_end = [n + 4 for n in corner_start]
# 選ばれた4x4ピクセルの値を上書き
if labels is None:
# ラベルを与えない場合 -> 0~1の間のランダムな値
image[corner_start[0] : corner_end[0], corner_start[1] : corner_end[1]] = (
random.uniform(0, 1)
)
else:
# ラベルを与えた場合 -> 255 - 25*(ラベルの値)
image[corner_start[0] : corner_end[0], corner_start[1] : corner_end[1]] = (
255 - 25 * labels[n]
) / 255
return decoy_images
# trainデータにdecoy処理を実行
X_train_decoy = create_decoy_mnist(images=X_train, labels=y_train, seed=42)
# decoy処理後のtrainデータ15個を可視化
fig, axes = plt.subplots(3, 5, figsize=(10, 5))
for i, ax in enumerate(axes.flatten()):
ax.imshow(X_train_decoy[i], cmap="gist_gray")
fig.show()
# testデータにdecoy処理を実行
X_test_decoy = create_decoy_mnist(images=X_test)
# decoy処理後のtestデータ15個を可視化
fig, axes = plt.subplots(3, 5, figsize=(10, 5))
for i, ax in enumerate(axes.flatten()):
ax.imshow(X_test_decoy[i], cmap="gist_gray")
fig.show()
# decoy処理をかけたXをtensor化
X_train_tensor = torch.tensor(
X_train_decoy.reshape(N_train, -1),
dtype=torch.float32,
requires_grad=False,
)
X_test_tensor = torch.tensor(
X_test_decoy.reshape(N_test, -1), dtype=torch.float32, requires_grad=False
)
y_train_tensor = torch.tensor(y_train, dtype=torch.int32, device="cuda")
y_test_tensor = torch.tensor(y_test, dtype=torch.int32, device="cuda")以下は上記処理で作成したDecoy MNISTデータです。(1枚目がtrain、2枚目がtest)
隅に加えられるノイズの濃さが、trainはラベルの数字と相関している(0は薄く、9は濃い)一方、testでは濃さは完全にランダムになっています。つまり、trainデータでの学習時に、ノイズの濃さからラベルを予測するようにモデルが学習してしまうと、testデータでの予測精度が悪くなってしまうことが予想されます。


ドメイン損失関数を定義する
この問題を回避するためのドメイン知識として、「画像の縁付近のピクセルには、予測のために必要な情報はほぼ存在しない」という知識を分析者が持っていると仮定します。
具体的には、28×28のピクセルのうち、内側にある20×20ピクセルはモデルに参照され、その外側のピクセルはあまり参照されない、というように設定します。
is_background = np.ones((28, 28))
# 中央の14×14セルは0に、それ以外の縁は1にする
is_background[4:24, 4:24] = 0
is_background = torch.tensor(is_background.reshape(-1)).float()
plt.imshow(is_background.reshape(28, 28).cpu(), cmap="OrRd")
この知識をドメイン損失関数$\phi$に落とし込む方法として、論文中では以下のような定式化を行なっていました。
$$
\phi_{background}(h, x) = ||\nabla_x h(x)||^2_b
$$
式中の$b$は、先ほど定義した外側のピクセルのみを対象とすることを意味しています。つまり、$\phi$として画像データ$x$の縁の値が変化したときの、ニューラルネットの出力$h_w(x)$の変化量(の2乗)を定義していることになります。
このようにすると、縁のピクセル値がニューラルネットの出力に与える影響が小さいほど、$\phi$が小さくなりドメイン知識に近くなる、ということになります。
事前学習
それでは、上記のドメイン損失関数を使って、ニューラルネットの事前学習を行います。今回のニューラルネットは隠れ層を2層とし、その次元はどちらも50としています。また、重みパラメータの事前分布はすべて$N(0, 10^2)$を使用しています。
変分推論を使用するため、確率的プログラミング言語(PPL)の1つであるPyroを使ってBNNをPyroを構築します。
(PyroによるBNNの構築方法は、書籍『Pythonではじめるベイズ機械学習入門』を参考にしています)
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt
import random
from tqdm import tqdm
import pyro
import pyro.optim
from pyro.nn import PyroModule, PyroSample
import pyro.distributions as dist
from pyro import poutine
from pyro.infer import SVI, Trace_ELBO, Predictive
from pyro.infer.autoguide import (
AutoDiagonalNormal,
AutoLowRankMultivariateNormal,
init_to_sample,
)
torch.set_default_device("cuda")
class BNN_pretrain(PyroModule):
"""BNNの事前学習"""
def __init__(self, hidden_dim1, hidden_dim2, out_dim):
super().__init__()
# 隠れ層1
self.fc1 = PyroModule[nn.Linear](784, hidden_dim1)
self.fc1.weight = PyroSample(
dist.Normal(0.0, 10.0).expand([hidden_dim1, 784]).to_event(2)
)
self.fc1.bias = PyroSample(
dist.Normal(0.0, 10.0).expand([hidden_dim1]).to_event(1)
)
# 隠れ層2
self.fc2 = PyroModule[nn.Linear](hidden_dim1, hidden_dim2)
self.fc2.weight = PyroSample(
dist.Normal(0.0, 10.0).expand([hidden_dim2, hidden_dim1]).to_event(2)
)
self.fc2.bias = PyroSample(
dist.Normal(0.0, 10.0).expand([hidden_dim2]).to_event(1)
)
# 出力層
self.fc3 = PyroModule[nn.Linear](hidden_dim2, out_dim)
self.fc3.weight = PyroSample(
dist.Normal(0.0, 10.0).expand([out_dim, hidden_dim2]).to_event(2)
)
self.fc3.bias = PyroSample(dist.Normal(0.0, 10.0).expand([out_dim]).to_event(1))
def forward(self, X, total_size, is_background, loss_scale):
input_dim = X.shape[0]
# 活性化関数はReLuを使用
z_h1 = F.relu(self.fc1(X))
z_h2 = F.relu(self.fc2(z_h1))
z_output = self.fc3(z_h2)
# 分類モデルなので、出力値をlog_softmax変換
score = F.log_softmax(z_output, dim=1)
out_dim = z_output.shape[1]
# 出力は10次元あるので、1つずつXによる勾配を計算し、リストに格納していく
# (もっといい方法あるかも)
grads = list()
for d in range(out_dim):
grad = torch.autograd.grad(
outputs=score[:, d],
inputs=X,
grad_outputs=torch.ones_like(score[:, d]),
create_graph=True,
)[0]
grads.append(grad)
X_grad = pyro.deterministic("X_grad", torch.stack(grads))
# 勾配のうち、縁部分に該当するピクセルの値のみ残す
X_background_grad = pyro.deterministic(
"X_background_grad", X_grad * is_background
)
# 損失として勾配の二乗平均を定義
# (1000で割っているのは、スケールを小さくしたかっただけでなくてもOK)
loss = pyro.deterministic(
"loss", X_background_grad.square().mean(axis=(0, 2)) / 1000
)
# 各サンプルごとに、損失のしたがう分布を定義
with pyro.plate("data", total_size, subsample_size=input_dim):
pyro.sample("prob", dist.Normal(loc=0.0, scale=loss_scale), obs=loss)
return loss事前学習を実行します。ハイパーパラメータ$\tau$の値として、いろいろ試した結果$10,000$を使用することにしました。
out_dim = 10
hidden_dim1 = 50
hidden_dim2 = 50
total_pretrain_size = X_train_tensor.shape[0]
pretrain_batch_size = 256
model = BNN_pretrain(hidden_dim1=hidden_dim1, hidden_dim2=hidden_dim2, out_dim=out_dim)
pyro.clear_param_store()
# 論文では低ランクの多変量正規分布で近似していたが、
# 今回は簡単化のため、共分散行列が対角行列の正規分布で近似
guide = AutoDiagonalNormal(model=model, init_loc_fn=init_to_sample())
adam = pyro.optim.Adam({"lr": 0.01})
svi = SVI(model=model, guide=guide, optim=adam, loss=Trace_ELBO())
pyro.set_rng_seed(123)
n_epoch = 20
losses = []
for _ in tqdm(range(n_epoch)):
dataloader = DataLoader(
TensorDataset(X_train_tensor),
batch_size=pretrain_batch_size,
shuffle=True,
generator=torch.Generator(device="cuda"),
)
for b in dataloader:
bx = b[0]
loss = svi.step(
X=bx.clone().requires_grad_(),
total_size=total_pretrain_size,
is_background=is_background,
# ハイパーパラメータtau
loss_scale=10000,
)
losses.append(loss)
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(losses)
ax.set_xlabel("epoch")
ax.set_ylabel("loss")
ax.set_yscale("log")
fig.show()事前学習中の損失の推移をチェックしても、いい感じに収束してそうです。
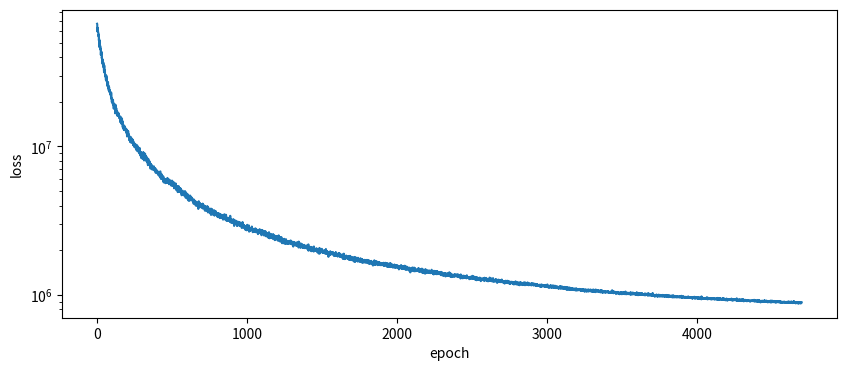
事前学習の結果、重みパラメータの事前分布の平均・標準偏差がどのようになったか、可視化して確認してみます。
その結果、平均(上段)のほうはあまり特徴はないですが、標準偏差(下段)のほうは、値が0に近いところ(=パラメータの事前分布が学習されているところ)と、10に近いところ(=事前学習を行っても、パラメータの事前分布が特に変化しなかったところ)に分かれていることがわかります。
# 事前学習後の事前分布の平均および標準偏差を取得
estimated_loc = pyro.param("AutoDiagonalNormal.loc").to("cpu").detach().numpy()
estimated_scale = pyro.param("AutoDiagonalNormal.scale").to("cpu").detach().numpy()
fig, axes = plt.subplots(2, 1, figsize=(10, 4), sharex=True)
axes = axes.flatten()
axes[0].fill_between(range(len(estimated_loc)), estimated_loc)
axes[1].fill_between(range(len(estimated_loc)), estimated_scale)
axes[0].set_title("loc")
axes[1].set_title("scale")
fig.show()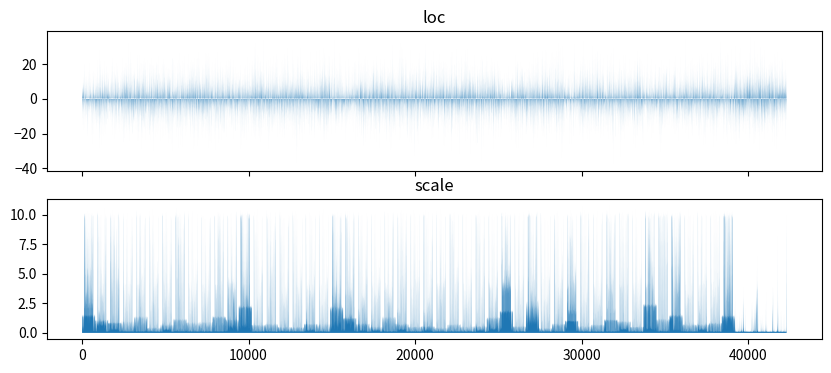
本学習
この結果を流用し、本学習を実行してMNIST分類モデルを作成します。
def extract_each_param(
all_param: torch.tensor, input_dim: int, out_dim: int, hidden_dims: list[int]
):
"""全層のパラメータがすべて格納された配列から、各層に対応したパラメータを取得する"""
n_layer = len(hidden_dims) + 1
weight_list = []
bias_list = []
total_params_until_prev_iter = 0
for i in range(n_layer):
if i == 0:
n_weight = input_dim * hidden_dims[0]
n_bias = hidden_dims[0]
elif i == n_layer - 1:
n_weight = hidden_dims[i - 1] * out_dim
n_bias = out_dim
else:
n_weight = hidden_dims[i - 1] * hidden_dims[i]
n_bias = hidden_dims[i]
start_idx_weight = total_params_until_prev_iter
end_idx_weight = start_idx_weight + n_weight
end_idx_bias = end_idx_weight + n_bias
weight_list.append(all_param[start_idx_weight:end_idx_weight])
bias_list.append(all_param[end_idx_weight:end_idx_bias])
total_params_until_prev_iter = end_idx_bias
return weight_list, bias_list
class BNN_main(PyroModule):
"""BNNによる画像分類モデル"""
def __init__(self, out_dim, hidden_dim1, hidden_dim2, loc, scale):
super().__init__()
# 事前学習後の全平均パラメータの配列から、各層のパラメータを取得
loc_weight, loc_bias = extract_each_param(
all_param=loc,
input_dim=784,
out_dim=out_dim,
hidden_dims=[hidden_dim1, hidden_dim2],
)
# 事前学習後の全標準偏差パラメータの配列から、各層のパラメータを取得
scale_weight, scale_bias = extract_each_param(
all_param=scale,
input_dim=784,
out_dim=out_dim,
hidden_dims=[hidden_dim1, hidden_dim2],
)
self.fc1 = PyroModule[nn.Linear](784, hidden_dim1)
self.fc1.weight = PyroSample(
dist.Normal(
loc_weight[0].reshape(hidden_dim1, 784),
scale_weight[0].reshape(hidden_dim1, 784),
).to_event(2)
)
self.fc1.bias = PyroSample(dist.Normal(loc_bias[0], scale_bias[0]).to_event(1))
self.fc2 = PyroModule[nn.Linear](hidden_dim1, hidden_dim2)
self.fc2.weight = PyroSample(
dist.Normal(
loc_weight[1].reshape(hidden_dim2, hidden_dim1),
scale_weight[1].reshape(hidden_dim2, hidden_dim1),
).to_event(2)
)
self.fc2.bias = PyroSample(dist.Normal(loc_bias[1], scale_bias[1]).to_event(1))
self.fc3 = PyroModule[nn.Linear](hidden_dim2, out_dim)
self.fc3.weight = PyroSample(
dist.Normal(
loc_weight[2].reshape(out_dim, hidden_dim2),
scale_weight[2].reshape(out_dim, hidden_dim2),
).to_event(2)
)
self.fc3.bias = PyroSample(dist.Normal(loc_bias[2], scale_bias[2]).to_event(1))
def forward(self, X, total_size, y=None):
input_dim = X.shape[0]
z_h1 = F.relu(self.fc1(X))
z_h2 = F.relu(self.fc2(z_h1))
log_prob = F.log_softmax(self.fc3(z_h2), dim=1)
with pyro.plate(name="data", size=total_size, subsample_size=input_dim):
pyro.sample("y", dist.Categorical(logits=log_prob), obs=y)
本学習を実行します。損失の推移も問題なさそうです。
total_train_size = X_train_tensor.shape[0]
train_batch_size = 256
model = BNN_main(
out_dim=out_dim,
hidden_dim1=hidden_dim1,
hidden_dim2=hidden_dim2,
loc=torch.tensor(estimated_loc, dtype=torch.float32, device="cuda"),
scale=torch.tensor(estimated_scale, dtype=torch.float32, device="cuda"),
)
pyro.clear_param_store()
# こちらは低ランク多変量正規分布で近似
guide = AutoLowRankMultivariateNormal(
model=model, rank=10, init_loc_fn=init_to_sample()
)
adam = pyro.optim.Adam({"lr": 0.01})
svi = SVI(model=model, guide=guide, optim=adam, loss=Trace_ELBO())
pyro.set_rng_seed(123)
n_epoch = 10
losses = []
for _ in tqdm(range(n_epoch)):
dataloader = DataLoader(
TensorDataset(X_train_tensor, y_train_tensor),
batch_size=train_batch_size,
shuffle=True,
generator=torch.Generator(device="cuda"),
)
for bx, by in dataloader:
loss = svi.step(
X=bx,
y=by,
total_size=total_train_size,
)
losses.append(loss)
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(losses)
ax.set_xlabel("epoch")
ax.set_ylabel("loss")
fig.show()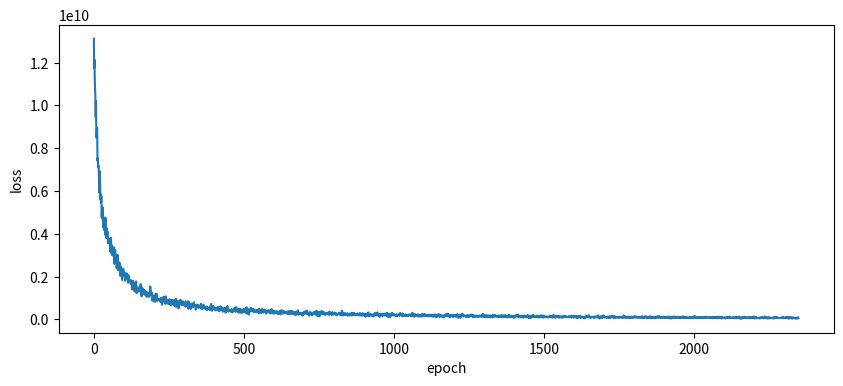
この本学習したモデルから、データ$X$をインプットとした際の$y$の予測値を100個サンプリングしてみます。そして、そのサンプル中の最頻値を、予測ラベルと定義します。
# 事後分布からyをサンプリング
pyro.set_rng_seed(123)
predictive = Predictive(model, guide=guide, num_samples=100)
y_pred_samples = predictive(
X=X_test_tensor,
total_size=total_train_size,
)["y"]
y_pred = y_pred_samples.mode(axis=0).values実際のラベルとのaccuracyを計算してみたところ、0.7889となりました。
from sklearn.metrics import accuracy_score, confusion_matrix
accuracy_score(y_test_tensor.cpu(), y_pred.cpu())
# -> 0.7889比較として、まったく同じ設定で普通のBNN(=事前学習なしで、重みの事前分布として$N(0, 10^2)$を使用したモデル)での精度も計算してみたところ、accuracyは0.7425でしたので、精度は若干向上しているといえそうです。
(どちらの手法も、ハイパラ等の細かいチューニングは行なっていませんので、参考まで)
その他の応用例
Decoy MNIST以外にも、論文中にはドメイン知識の適用例がいくつかありましたので簡単にご紹介します。
(※1つ目の例は、ドメイン知識によって精度をあげたいというよりも、機械学習モデルが人種間で異なる出力をしないようにしたい、というモチベーションのようです)
| 応用先タスク | 適用するドメイン知識 | 損失関数$\phi$ |
|---|---|---|
| 求人に対する応募者の属性データ+実際に採用されたかのオープンデータを用い、採用有無の予測モデルを作成 | 黒人か白人かで、予測モデルの出力に差は生じない | $\phi=($黒人の場合の予測採用確率$ – $白人の場合の予測採用確率$)^2$ |
| 血圧管理のための介入が必要かどうかの二値分類モデルを作成 | 介入が必要な人の条件が、経験的にわかっている (乳酸値が高い、血液ガス測定値が高い、etc…) | $\phi=\mathbf{1}[x\in$ 経験的に介入が必要とされる条件の値域$] \cdot \text {ReLu}(1-h(x))$ |
| 二重振り子の次の状態を、直前の状態をインプットとして予測するモデルを作成 | 摩擦によって、予測時点の総エネルギーは、インプット時点の総エネルギーよりも小さくなるはず | $\phi = \text{max}( E(h(x)) – E(x), 0)$ |
まとめ
今回は、BNNに分析者がもつドメイン知識を組み込む方法をご紹介しました。「事前分布を学習させる」という処理が、ベイズの思想的にどうなんだろう?とは思ったものの、予測精度をあげるためのアプローチとしてはありかなと個人的には考えています。
一方で、以下の点については各タスクに対して都度設定する必要があるため、分析者の腕が試されるポイントなのかなと感じました。
- ドメイン損失関数$\phi$の設計
- ドメイン知識が複数ある場合の組み込み方法
- ハイパーパラメータ$\tau$の値の設定
あと余談ですが、私があまりPyTorchに慣れてないこともあり、今回の実装はかなり苦労しました。。。実装について何かおかしい点があれば、ご指摘いただけると幸いです。
参考:
- 論文『Bayesian Neural Networks with Domain Knowledge Priors』
- 書籍『Pythonではじめるベイズ機械学習入門』
- Pyroフォーラム『Subsampling vs batching』
- Qiita記事『PyTorchで高階偏微分係数』