本記事は、R言語 Advent Calendar 2023および確率的プログラミング言語 Advent Calendar 2023の21日目の記事です。どちらもアドベントカレンダーも空きがありましたので投稿させていただきました。「1つの記事で2つのアドベントカレンダーに投稿する」という横着をお許しください。
(調べた限りでは問題はなさそうでしたが、もしマナー的によろしくないというご指摘があれば、どちらかのアドベントカレンダーから削除いたします)
はじめに
株価や為替レートなどの金融資産の分散(=ボラティリティ)は通常一定ではなく、時間と共に変動します。つまり、価格が小さい変化しかしない時期もあれば、急騰・下落のような大きな変化が続く時期も存在します。このボラティリティの時間変動を表すモデルが確率的ボラティリティモデル(Stochastic Volatility model, SVモデル)です。
今回は、このSVモデルをstanで実装してみます。
記事を書くきっかけ
最近知ったのですが、株価の相場指標の一つとしてボリンジャーバンドというものがあるそうです。
ボリンジャーバンドを一言で言うと「株価が収まるであろう範囲」のことで、以下の式で表現されます。
過去20日間の株価の平均 ± 2 × 過去20日間の株価の標準偏差
いわゆる『平均 $\pm \sigma$』の式になっています。「株価は平均$\pm \sigma$の範囲に収まるだろう」という見方をし、逆に株価がこのボリンジャーバンドより外側にあれば、「株価が異常な価格上昇or下落をしているのでは?」と見なすことができます。
計算もシンプルで、かつ不確実性の大きさの観点も含んでいるため、投資ド素人の私がこの指標の存在を知ったときは「こんな便利な指標があったんだな〜」という感想を持ちました。
ただしこの式を見たときに、「時系列データの標準偏差って、(厳密には)こんな簡単な計算では求められないのでは?」→「厳密に求めるには、SVモデルを使う必要がありそう」→「アドベントカレンダーにも空きがあるし、stanでSVモデルを実装してみようかな」と思った次第です。
注意:あくまでSVモデルによる標準偏差の求め方を紹介するのが本記事の目的であり、ボリンジャーバンドを否定するものではありません。(ボリンジャーバンド自体はとても有用な指標だと思います)
SVモデルとは?
SVモデルは以下の状態空間モデルで表現されます。(stochvolというRパッケージのマニュアルに準拠)
$$
\begin{gather}
\begin{cases}
y_t = \mathbf{X_t} \boldsymbol{\beta} + \exp(h_t / 2) \varepsilon_t \\
h_t = \mu + \phi(h_{t-1} – \mu) + \sigma \eta_t
\end{cases} \\
\varepsilon_t \sim N(0, 1),\ \eta \sim N(0, 1)
\end{gather}
$$
$y_t$は時点$t$における株価、$\mathbf{X_t}$は共変量、$\beta$は回帰係数です。その誤差項は$\varepsilon_t \sim N(0,1)$より、$\exp(h_t / 2)\varepsilon_t \sim N(0, \exp(h_t))$となります。
つまり、$h_t$が大きいほど$y_t$の分散が大きく、逆に$h_t$が小さいほど$y_t$の分散が小さいことを意味します。($h_t$自体はマイナスの値も取り得るので、$\exp$をつけて正の値に変換したものを分散として扱っています)
この$\exp(h_t)$がボラティリティ、$h_t$が対数ボラティリティに該当します。本モデルでは、対数ボラティリティ$h_t$を状態変数として扱っています。
2つ目の式はその$h_t$の時間変動を数式化した状態方程式で、AR(1)モデルを仮定しています。係数$\phi$はARモデルの定常性のために$-1<\phi < 1$の範囲の値をとる必要があり、かつ金融の世界では一般的に1に近い値をとるとされています。
今回実装はしませんが、SVモデルには目的変数を対数収益率$r_t = \log(y_t) – \log(y_{t-1})$にした、以下のようなバージョンも存在します。
(むしろこっちの方がSVモデルとしてはメジャーかも)
$$
\begin{gather}
\begin{cases}
r_t = \exp(h_t / 2) \varepsilon_t \\
h_t = \mu + \phi(h_{t-1} – \mu) + \sigma \eta_t
\end{cases} \\
\varepsilon_t \sim N(0, 1),\ \eta \sim N(0, 1)
\end{gather}
$$
Rでの実装
ではRでSVモデルを実装してみます。今回はcmdstanrを使用してstanでのMCMCを実行します。(cmdstanrのインストール手順はこちら)
# パッケージ読み込み
library(tidyverse)
library(patchwork)
library(cmdstanr)
library(bayesplot)
library(tidybayes)
library(tidyquant)
library(zoo)データはNVIDIA社の2022年以降の株価(終値)を使います。tidyquantパッケージを使って株価データを取得します。ついでにボリンジャーバンドの計算も実行します。
(余談:ボリンジャーバンドの計算コードはChatGPTのGPT-4に教えてもらいました)
# NVIDAの株価を取得しボリンジャーバンドを算出
df <- tq_get("NVDA", from = "2022-01-01") %>%
mutate(
ma = rollmean(close, 20, fill = NA, align = "right"),
sd = rollapply(close, 20, sd, fill = NA, align = "right")
) %>%
mutate(
upr_band = ma + 2 * sd,
lwr_band = ma - 2 * sd
)
# 株価の推移 & ボリンジャーバンドを可視化
g_bollinger <- ggplot(df, aes(x = date)) +
geom_line(aes(y = close)) +
geom_line(aes(y = ma), color="green4") +
geom_ribbon(aes(ymin = lwr_band, ymax = upr_band), fill="green4", alpha = 0.3) +
theme_minimal()
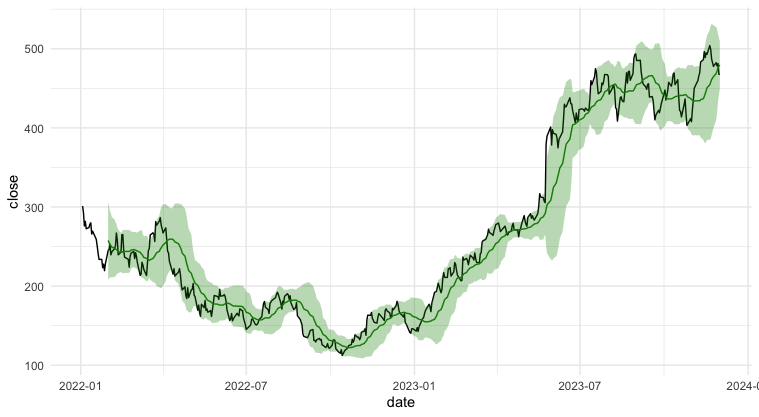
g_bollinger以下が株価推移 & ボリンジャーバンドの可視化結果です。緑色の線が過去20日間(当日含む)の移動平均、緑色の範囲がボリンジャーバンドになります。株価が急激に変化しているタイミング(2023年5月末あたりなど)には、ボリンジャーバンドも広くなっていることが分かります。
このデータをもとに、SVモデルを実装してみます。今回は以下のようなモデルを考えてみました。
$$
\begin{gather}
\begin{cases}
y_t = \sum_{p=1}^{19} \psi_p y_{t-p} + \exp(h_t / 2) \varepsilon_t \\
h_t = \mu + \phi(h_{t-1} - \mu) + \sigma \eta_t
\end{cases} \\
\varepsilon_t \sim N(0, 1),\ \eta_t \sim N(0, 1), \\
\psi_1,\dots,\psi_{19} \sim Dir((100,\dots,100)), \\
\mu \sim N(0, 10), \\
\phi \sim TN_{(-1,1)}(0.9, 0.1), \\
\sigma \sim N^+(0, 1)
\end{gather}
$$
$y_t$の平均として、ボリンジャーバンドに倣い過去19日の加重平均を使用します。その重み$\psi_1, \dots, \psi_{19}$の事前分布としてディリクレ分布$Dir((100,\dots,100))$を設定しています。ディリクレ分布を使用することで、$\psi_1,\dots,\psi_{19}$は全て非負かつその合計が1になります。ハイパーパラメータを100にしているのは、各重みの値をなるべく同じ大きさにし、$y_t$の平均が滑らかになるようにしたかったからです。(値を大きくするほど近い値が、0に近いほどバラバラの値がでやすい)
$Dir((1,\dots,1))$でも試してみたのですが、$\psi_1$だけが1にかなり近い値を取り、$y_t$の平均≒$y_{t-1}$と、ほぼ前日の値を引き継ぐだけの結果となりました。
$\phi$の事前分布は、切断正規分布$TN_{(-1, 1)}(0.9, 0.1)$にしています。これは、「$\phi$の値は一般的に1に近い値をとる」という前提知識を反映しています。
その他のパラメータの事前分布については、特に意図はなく適当にハイパーパラメータを設定しています。
これらのモデルを、以下のようにstanファイルに記述します。Logics of Blueさんの記事『状態空間モデルをStanで推定するときの収束を良くするコツ』を参考に、再パラメータ化を使い収束しやすくなるよう記述しています。
またgenerated quantitiesブロックを使い、事後予測分布からのサンプルもまとめて生成するようにしてます。
data {
// 時系列データの数
int T;
// 加重平均に用いる過去データの数
int n_past;
// インプットデータ
vector[T + n_past] y_org;
}
transformed data {
// 最初のn_past個は目的変数として使えないのでドロップ
vector[T] y;
y = y_org[(1+n_past):(T+n_past)];
}
parameters {
// hの平均
real mu;
// hの係数
real phi;
// 過去データの加重平均に使う重み(合計1になる)
simplex[n_past] psi;
// hの誤差項
vector[T] err_h;
// hの標準偏差
real sigma_h;
}
transformed parameters {
// 状態変数h
vector[T] h;
// yの平均
vector[T] mean_y;
// yの標準偏差
vector[T] sd_y;
for(t in 1:T){
// hはt==1かそれ以外かで場合分け
if(t == 1){
h[1] = mu + (sigma_h / sqrt(1-phi^2) ) * err_h[1];
}
else{
h[t] = mu + phi * (h[t-1] - mu) + sigma_h * err_h[t];
}
// mean_yは過去n_past個のデータの加重平均
mean_y[t] = dot_product(psi, y_org[t:(t+n_past-1)]);
// sd_yは状態変数hに0.5をかけて指数変換
sd_y[t] = exp(0.5 * h[t]);
}
}
model {
y ~ normal(mean_y, sd_y);
err_h ~ normal(0, 1);
phi ~ normal(0.9, 0.1);
mu ~ normal(0, 10);
sigma_h ~ normal(0, 1);
// 重みはなるべく等しい値にしたいので、ディリクレ分方のハイパーパラメータは大きな値を設定
psi ~ dirichlet(rep_vector(100, n_past));
}
generated quantities {
// yの予測分布からのサンプル
vector[T] y_pred;
for(t in 1:T){
y_pred[t] = normal_rng(mean_y[t], sd_y[t]);
}
}
このモデルをcmdstanr_sv.stanという名前で同じディレクトリに配置し、コンパイルした後MCMCを実行します。私の環境では40秒くらいで終わりました。
# モデルコンパイル
model <- cmdstan_model("cmdstanr_sv.stan")
# 加重平均の重みの数
n_past <- 19
# cmdstanに渡すデータのリスト
data <- list(T = nrow(df) - n_past, n_past = n_past, y_org = df$close)
# MCMC実行
fit <- model$sample(
data = data,
seed = 123,
iter_warmup = 2000,
iter_sampling = 4000,
thin = 1,
chains = 4,
parallel_chains = 4,
refresh = 500,
)MCMCが終了したら、Rhatにて収束状況を確認します。1.1以下であればOKと言われているので、今回は収束は問題なさそうです。
# Rhatの可視化
rhat(fit) %>% mcmc_rhat()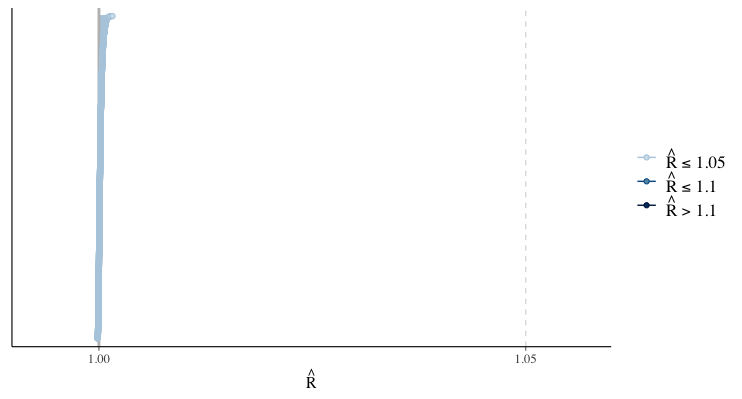
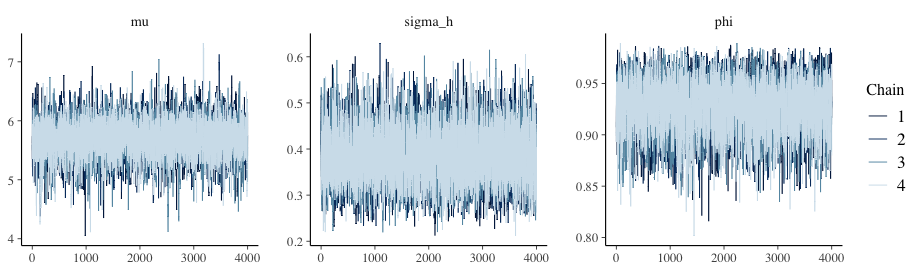
MCMCの結果をより扱いやすくするために、データフレーム形式で取得します。その後、代表的なパラメータのトレースプロットを確認してみます。
# MCMCサンプルをデータフレームで取得
draws <- fit$draws(format = "df")
# 各パラメータのトレースプロットを描画
mcmc_trace(draws, pars = c("mu", "sigma_h", "phi"))
mcmc_trace(draws, regex_pars = c("psi"))トレースプロットで見ても、収束は問題なさそうです。
ではMCMCサンプルから、事後予測分布からのサンプルy_predを抽出し、事後中央値およびHDIを求めます。ただし、MCMCサンプルをまとめたデータフレームdrawsは、以下のようにy_pred[1], y_pred[2], ...のMCMCサンプルが列ごとに分かれて格納されており、このままでは若干扱いにくいです。
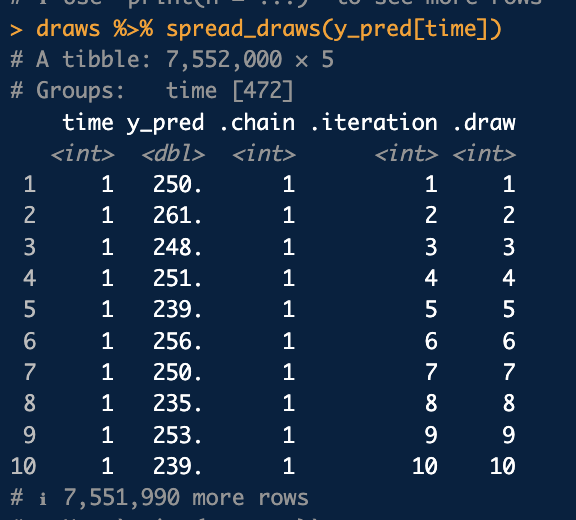
そこで、tidybayesパッケージのspread_draws関数を使います。この関数を使うことで、縦持ちのデータフレームにしつつ、変数名からのインデックスの抽出(=y_pred[1], y_pred[2], ...から、インデックスを表す文字列1, 2, ...だけを取得する)も同時に行ってくれます。
以下のようにspread_draws(y_pred[time])と渡すことで、使いやすい形式のデータフレームになってくれていることがわかります。(y_pred[time]のtimeの部分は適当な名前でOKです)
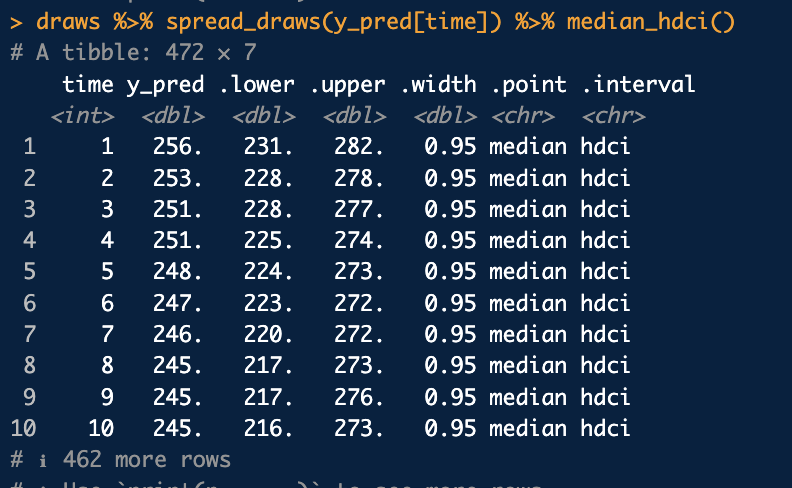
中央値およびHDIを求めるには、このデータフレームをtimeでgroup_byし適切な関数を使えばOKです。が、実はtidybayesパッケージのmedian_hdci関数に投げるだけで、各timeごとの中央値およびHDIを勝手に計算してくれます。
(厳密には、tidybayesパッケージが内部で呼び出しているggdistパッケージに含まれる関数のようです)
madian_hdci関数では、中央値およびHDIを自動で一辺に求めてくれますが、他にも以下のように様々なバリエーションがあります。
| 関数 | 算出する値 |
|---|---|
mean_qi | 平均値および分位点区間 |
median_qi | 中央値および分位点区間 |
mode_qi | 最頻値および分位点区間 |
mean_hdi | 平均値およびHDI (多峰の場合は複数の区間を算出) |
median_hdi | 中央値およびHDI (多峰の場合は複数の区間を算出) |
mode_hdi | 最頻値およびHDI (多峰の場合は複数の区間を算出) |
mean_hdci | 平均値およびHDI (多峰の場合でも単一の区間のみ算出) |
median_hdci | 中央値およびHDI (多峰の場合でも単一の区間のみ算出) |
mode_hdci | 最頻値値およびHDI (多峰の場合でも単一の区間のみ算出) |
分位点区間(別名ETI)とHDIの定義・性質については、以前書いたこちらの記事をご覧ください。
では、spread_drawsとmedian_hdciを活用し、事後予測分布からのサンプル取得 & 中央値およびHDI区間を算出を行い、さらにその結果を可視化してみます。
y_pred <- draws %>%
spread_draws(y_pred[time]) %>%
# memo:median_hdi()だとmultimodalのときに複数の区間を算出してしまうので今回は使わない
median_hdci() %>%
mutate(date = tail(df$date, nrow(df) - n_past))
g_sv <- ggplot(y_pred, aes(x = date)) +
geom_line(aes(y = y_pred), color = "royalblue") +
geom_ribbon(aes(ymin = .lower, ymax = .upper), fill = "royalblue", alpha = 0.3) +
geom_line(mapping=aes(x = date, y = close), data = df) +
theme_minimal()
g_sv以下が事後予測の結果です。青塗りつぶしのHDIが広いほど、ボラティリティの値が大きいという解釈になります。例えば、株価が大きく上昇した2023年5月末あたりはボラティリティが増加したため、HDIも広くなっています。
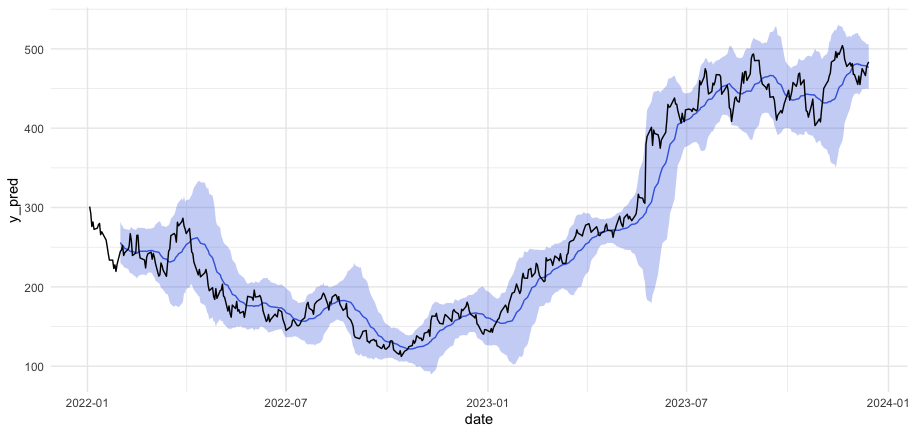
SVモデルの結果とボリンジャーバンドを並べて可視化してみます。大まかには同じような動きをしていますが、SVモデルで推定したボラティリティのほうが、ボリンジャーバンドより広い傾向にあるようです。
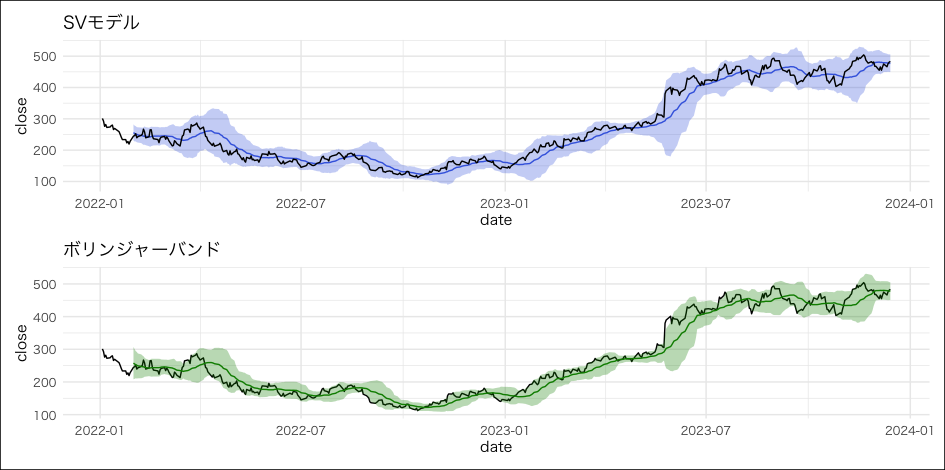
ただし、ボリンジャーバンドは直近20日間の価格をもとに算出している一方、SVモデルでは全期間の価格をもとにボラティリティを推定しています。例えば、2023/4/20のボラティリティを計算する場合、ボリンジャーバンドでは2023/3/23~4/20の20日間のデータ(※土日祝日を除く)だけを使用する一方、SVモデルでは過去・未来含む全てのデータ(今回のデータだと、2022/1/3~2023/12/14)を使ってボラティリティを推定しています。
つまりこの2つは算出の際の前提条件が異なるため、今回の結果を見てどっちがどうという比較を行うことは(厳密には)できません。特にSVモデルでは、本来知り得るはずのない未来のデータを使用しており、当然SVモデルによるボラティリティのほうがより実際のデータにフィットした結果になるはずです。
もし同じ条件で比較したいのであれば、SVモデルにおける状態変数$h_t$を、MCMCではなくフィルタリングで推定する必要があります。そうすれば、「過去のデータだけを用いてボラティリティの計算を行う」という条件は揃えられます。
ただし、SVモデルは線形ガウス状態空間モデルでないため、カルマンフィルタが使用できません。このような非線形or非ガウスの状態空間モデルのフィルタリングを行うには、粒子フィルタなどの手法を使う必要があります。
今回は粒子フィルタの実装がめんどくさいため確率的プログラミング言語アドベントカレンダーへの投稿となるため、stanによるMCMCを使った推定方法のみご紹介いたしました。
まとめ
今回は、stan(cmdstanr)によるSVモデルの実装方法をご紹介いたしました。tidybayesパッケージについて、正直私もあまり使い慣れていないのですが、うまく使いこなさせればcmdstanrの結果を楽にハンドリングできそうなので、今後も便利な使い方を探っていこうと思います。
参考:
- Rパッケージ『stochvol』『factorstochvol』のマニュアル
- Logics of Blueさんの記事『状態空間モデルをStanで推定するときの収束を良くするコツ』
- マネックス証券 ボリンジャーバンド解説