HDIとは?
ベイズ統計では、MCMCで発生させたサンプルを用いて、各変数の取り得る値の区間を計算することがあります。
例を以下のシンプルな単回帰で考えてみます。
\begin{gather}
y_i = \alpha + \beta x_i + \varepsilon_i, \\
\alpha \sim N(\mu_\alpha,\ \sigma_\alpha^2), \\
\beta \sim N(\mu_\beta,\ \sigma_\beta^2)
\end{gather}
($\mu_\alpha, \sigma_\alpha, \mu_\beta, \sigma_\beta$は適当な定数)
MCMCでモデル内のパラメータ$\alpha, \beta$をサンプリングしたとします。
もし「説明変数$x_i$は目的変数$y_i$に正の効果を与えるのか?」を検証したい場合、$\beta$のサンプルから95%信用区間(注:信頼区間ではないです!!)を計算します。
そしてその95%信用区間(以下、信用区間をCIと表記します)が0より大きい範囲に入っているかを調べる、という手順を踏みます。
ベイズ版の仮説検定ですね。
ある幅のCI(一般的に表記すると100$\alpha$%CI)の計算で最も一般的なのは、サンプルを値の大きさで並びかえ、小さいほうから数えて$100\times(1-\alpha)/2$%にあたる点を下限、大きいほうから数えて$100\times(1-\alpha)/2$%にあたる点を上限に設定する方法です。
(例えば、1,000個のサンプルから95%CIを計算する場合、昇順で25番目の値をCIの下限、降順で25番目の値をCIの上限として用いる)
この方法によって計算されたCIは、ETI(Equal Tailed Interval)とかCentral Intervalと呼ばれているらしいです。
名前自体は知らなくても、普段この定義の信用区間を使用している方は多いと思います。私も名前は最近知りました。
ただ、このETIにはひとつ問題があります。それはCIの区間外の値のほうが、区間内の値よりも取りやすいという事態が生じ得るという点です。
例を使って説明します。
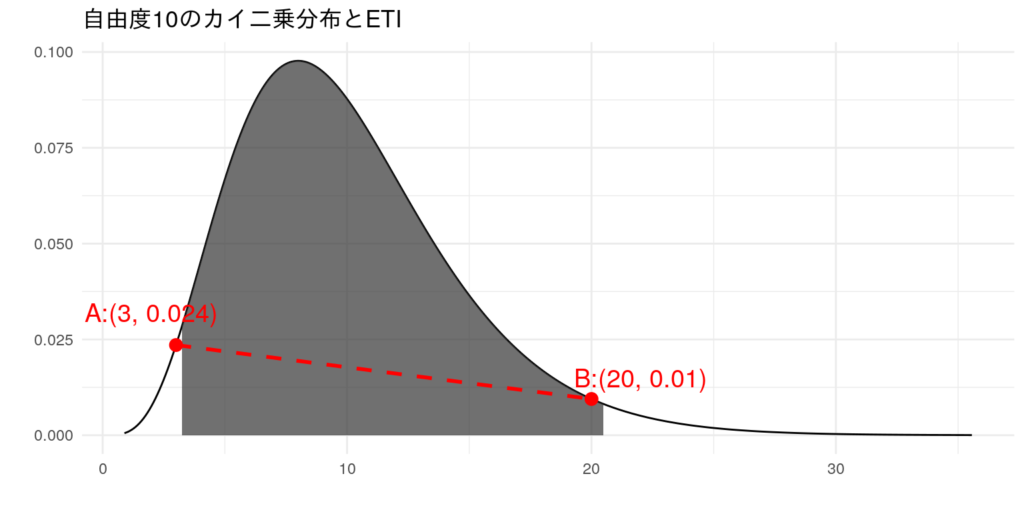
以下は自由度10のカイ二乗分布の確率密度関数(pdf)です。95%ETIを黒く塗りつぶしています。
これを見ると、CIの外にある点A(3, 0.024)のほうが、CI内である点B(20, 0.01)より高い位置にあります。つまり、CIの中にある点Bよりも、CIの外にある点Aのほうが確率的に取りやすいことになります。これってちょっと違和感ないですか?
この違和感を取り除けるのがHDIです。正式名称はHighest Density Intervalで、Highest Posterior Density区間(HPD区間)という別名もあります。
100$\alpha$%のHDIの定義は、「確率変数を確率密度が高いものから順に100$\alpha$%になるまでカバーしている区間」です(参考:『ウェブ最適化ではじめる機械学習』)。
数学的に厳密な定義は別にあるんですが、この定義から、先ほどの「CI外の点のほうがCI内の点よりも上にある」問題が回避できること分かるかと思います。
また、副産物として「いろんな定義のCIの中で、HDIは区間の幅が最小になるCIである」という性質も持っています(概説は後述)。
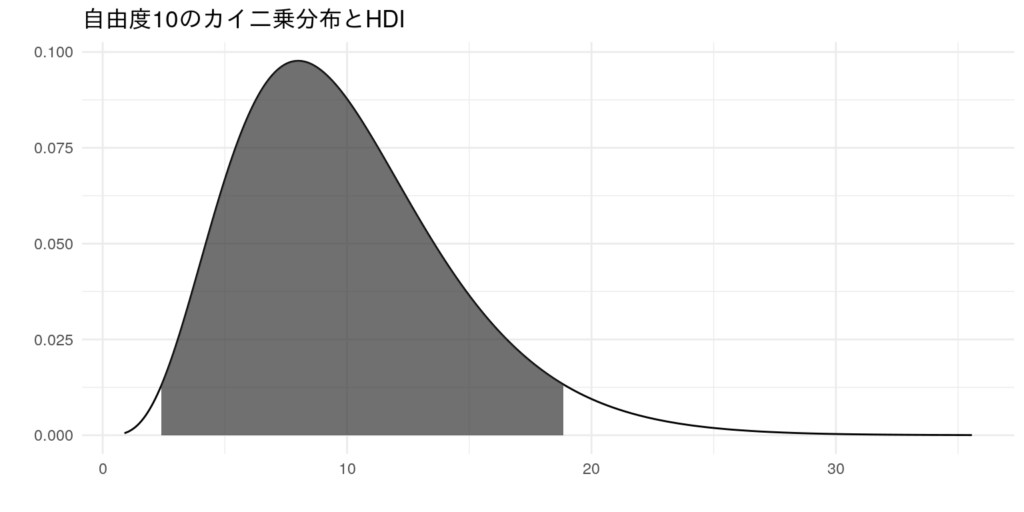
先ほどの自由度10のカイ二乗分布で、95%HDIを可視化すると以下のようになります。
CI内の点はすべてCI外の点より確率密度が高い位置にあり、かつCIの幅もETIのものより狭まっているのが見て取れます。
これだけ見ると「HDIええやん!!」となるんですが、計算がめんどくさいというデメリットもあります。ETIは並び替えて順番を数えるだけでいいので、それに比べたら手間ではありますよね。
また、分布が単峰でない(=分布の山が2つ以上ある)場合、CIが複数個に分割してしまい、計算や扱い方がより難しくなってしまうというデメリットもあります。
が、このようなケースは実用上あんまりないと思うので、個人的にはこのデメリットはそこまで問題ないかなと考えています。
bayestestRパッケージでHDIを計算する
上述のとおりHDIは計算がめんどいので、パッケージにお任せしちゃいます。
私が調べた限りでは、
bayestestRパッケージのhdi関数HDIntervalパッケージのhdi関数
の2つが使えそうでした。
今回はHDIの計算以外にもいろんな用途がある(らしい)bayestestR版を使用しますが、純粋にHDIを計算したいだけならHDInterval版でも大丈夫です。
まず、パラメータ(3, 15)のベータ分布にしたがう変数を生成します。rbeta関数での乱数生成ではなく、bayestestRにあるdistribution_beta関数で等間隔の分位点を作成します。
library(tidyverse)
library(bayestestR)
library(see)
library(ggthemes)
library(patchwork)
theme_set(theme_minimal(base_family = "HiraMaruProN-W4"))
alpha <- 3
beta <- 15
x = distribution_beta(10000, alpha, beta) # 等間隔の分位点を作成
y = dbeta(x, alpha, beta) # xに対応する密度を計算
df = tibble(x=x, y=y) # データフレームに格納
ggplot(df, aes(x = x, y = y)) +
geom_line() +
labs(x = "", y = "", title = paste0("Beta(", alpha, ", ", beta, ")"))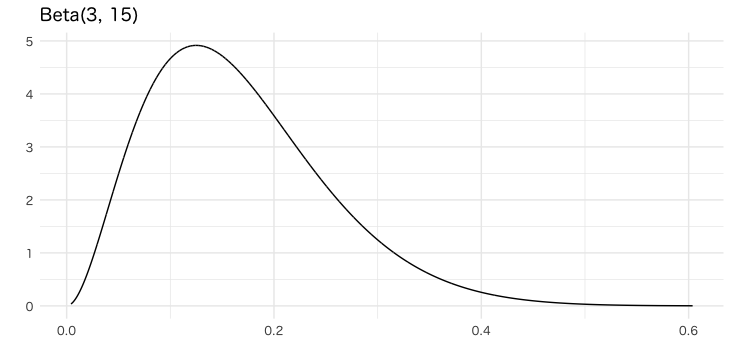
このxをhdi関数に渡すと、HDIの下限・上限が得られます。また結果はデータフレームとして扱える形式になっています。
デフォルトだと95%区間を計算してくれますが、今回は後のETIとの比較がしやすい70%に設定しました。
hdi = hdi(x, ci=0.70)
hdi## 70% HDI: [0.06, 0.22]
これをプロットしてみます。
df_hdi = df %>%
filter(x >= hdi$CI_low & x <= hdi$CI_high)
g_hdi <- ggplot() +
geom_line(data = df, mapping = aes(x = x, y = y)) +
geom_ribbon(data = df_hdi, mapping = aes(x = x, ymax = y, ymin = 0), fill = "blue", alpha = 0.5) +
labs(x = "", y = "", title = paste0("Beta(", alpha, ", ", beta, ")の70%HDI"))
g_hdi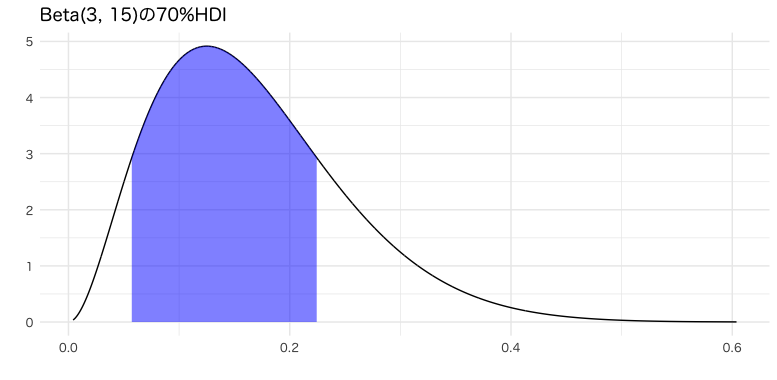
比較のため、ETIも可視化します。これもbayestestRパッケージにあるetiという関数で計算できます(べんり)。
eti = eti(x, ci=0.70)
df_eti = df %>%
filter(x >=eti$CI_low & x <= eti$CI_high)
g_eti = ggplot() +
geom_line(data=df, mapping=aes(x=x, y=y)) +
geom_ribbon(data=df_eti, mapping=aes(x=x, ymax=y, ymin=0), fill="red", alpha=0.5) +
labs(x="", y="", title=paste0("Beta(", alpha, ", ", beta, ")の70%ETI"))
g_eti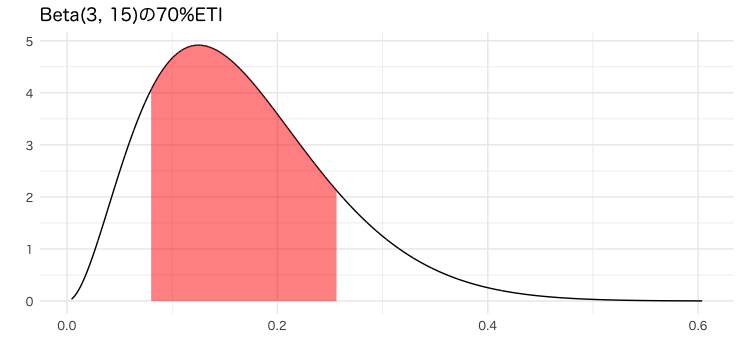
HDIとETIを並べてみると、以下の違いが見て取れますね。
- HDIでは確率密度の高い0近辺を含んでいるが、ETIでは含んでいない
- HDIのほうが区間の幅が短い
g_hdi / g_eti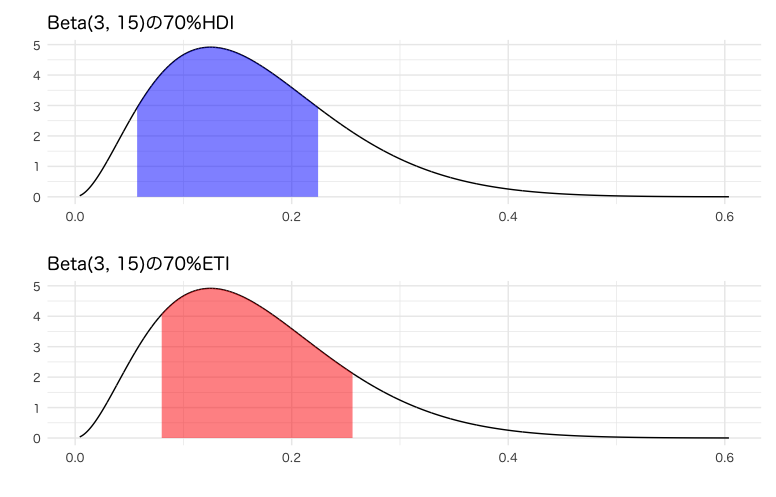
ちなみにhdiの結果をplot関数に渡すだけで、似たような図を自動で作成してくれます。
ただし、実際のベータ分布とは異なり、負の領域にも密度が存在している点は注意です(密度を機械的に推定してるので仕方ない)。
hdi(x, ci=0.70) %>%
plot()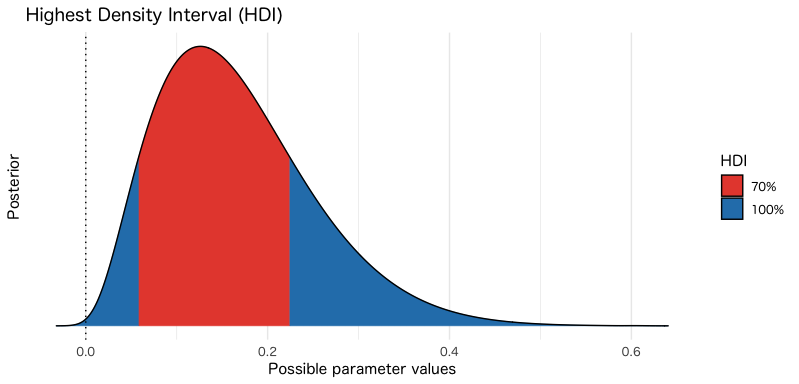
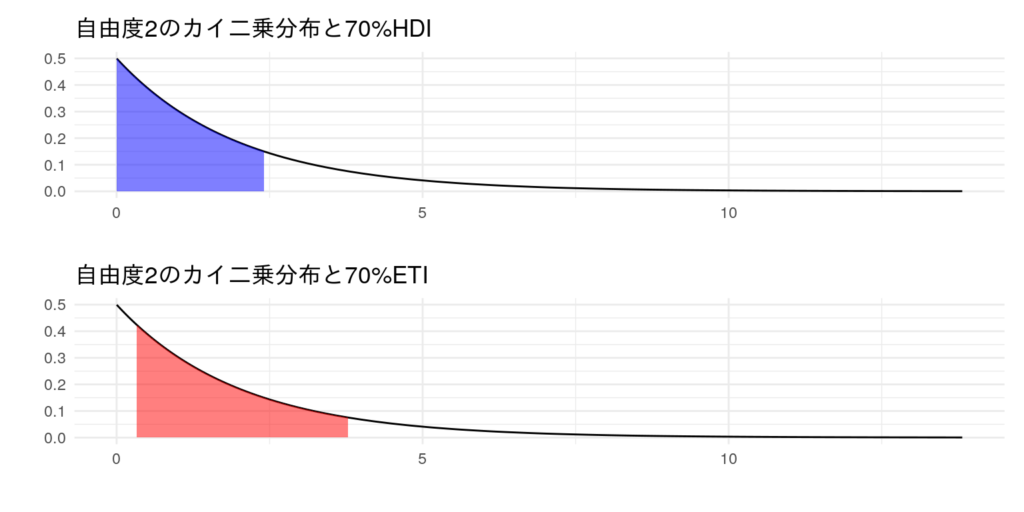
自由度2のカイ二乗分布(=平均2の指数分布)でも、同じようにHDI & ETIを可視化してみます。こちらのほうが幅の違いが顕著ですね。
HDIの幅が最小になる理由
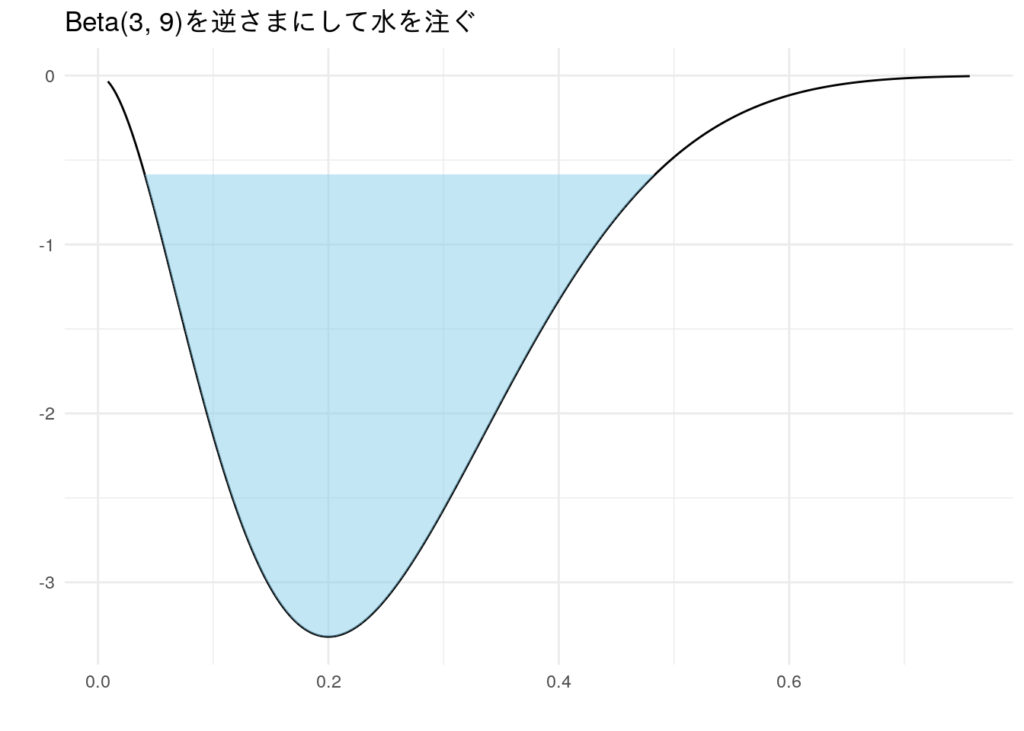
Machine Learning: a Probabilistic Perspectiveという本では、密度関数を上下反転させたものを"器"とみなし、この器に水を注ぐことをイメージすれば理解できる、と説明されています。
つまり、100$\alpha$%の容量の水を容器に注ぐと、深いところ(=密度が大きいところ)から水が溜まっていくため、水に浸かっていない部分は必然的に水面より高い場所(=密度が小さい場所)になります。
このように無駄のない埋め方をしているので、幅(水面の長さ)が最小になる、ということかと。(合ってるかな...)
ベータ分布$Beta(3,9)$を例に、水を注ぐイメージを可視化したのが以下です。
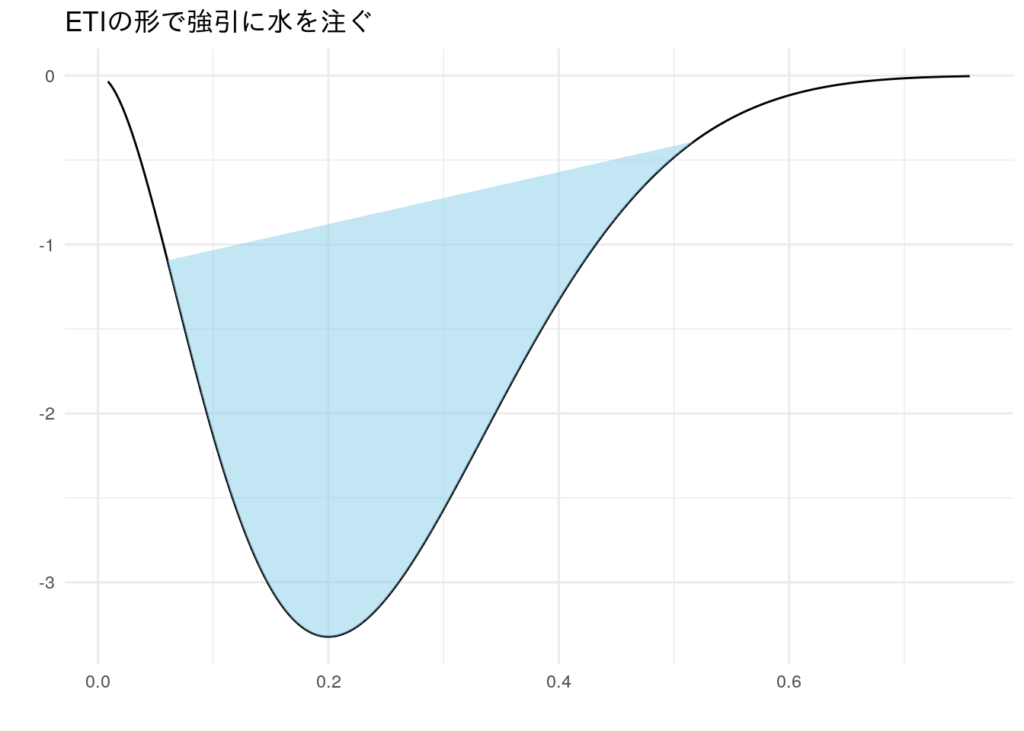
ETIも逆さまにして可視化してみます。水の溜まり方が不自然で、水面の幅がHDIより長くなってます。
まとめ
- HDIはETIよりも有用な点がある
- 計算が面倒だが、パッケージに任せれば簡単便利
ぜひHDIを使ってみてください!!
おまけ:HDIの幅が最小になる理由(詳細版)
注:私が自分で考えた証明なので、間違ってたらごめんなさい…。
以下を仮定・定義します。
- 1次元の確率変数$X$について考える
- $X$の確率密度関数pdfを$f(x)$、累積分布関数cdfを$F(x)$と表記する
- 分布は単峰(=山が1つだけ)
- 信用区間CIは区間$[a,b]$で、この区間内に最頻値(=分布の頂点)がある
- 区間$[a, b]$内では、常に$f(x)>0$
このとき、HDIの定義は以下になります。
- $F(b)-F(a)=\alpha$
- $f(a)=f(b)$
1番目はCIそのものの定義、2番目はHDI特有の定義です。
ここで、CIの長さ$b-a$の最小化を考えます。
先ほどの1番の式を制約条件として、以下の$G$にラグランジュ未定乗数法を適用します。($\lambda$はラグランジュ乗数)
$$
\begin{align}
G = b - a - \lambda (F(b) - F(a) - \alpha) \\
\Rightarrow\begin{cases}
\frac{\partial G}{\partial a} = -1 + \lambda f(a) = 0 \\
\frac{\partial G}{\partial b} = 1 - \lambda f(b) = 0 \\
\end{cases}
\end{align}
$$
$\lambda$を消去して、
$$
\begin{align}
\frac{1}{f(a)} &= \frac{1}{f(b)} \\
\therefore f(a) &= f(b)
\end{align}
$$
よって区間の幅$b-a$が最小となるのは$f(a)=f(b)$のときということが分かりました。
これはHDIの定義と一致するので、HDIが幅最小になるこということになります。