本記事は、『確率的プログラミング言語 Advent Calendar 2023』の15日目の記事になります。(アドベントカレンダーを主催していただいた松浦さんに感謝です!!)
今回は、論文『Log-Regularly Varying Scale Mixture of Normals for Robust Regression』で提案されている、外れ値を含んだデータの回帰分析に有用な“自由度0”のt分布と、Numpyroでの実装方法をご紹介します。
一般的な回帰分析
一般的なベイズ(線形)回帰分析では、以下の式を考えます。
$$
\begin{gather*}
y_i = \alpha + \sum_{k=1}^Px_{i,k}\beta_k + \varepsilon_i \ (i=1,\dots,N) \\
\varepsilon_i \sim N(0, \sigma^2)
\end{gather*}
$$
ただし、分析を当てはめるデータに外れ値が含まれていた場合、誤差項$\varepsilon_i$の分布に正規分布を用いると、$\alpha$や$\beta_k$の推定に大きく影響してしまうことがあります。
例として、以下のグラフのようなデータを考えます。真の回帰直線(青い線)から人工的にデータを生成します。その際、外れ値として意図的に約1割のデータを、青い線から大きく離れたものにしてみます。
このデータに最小二乗法を適用し推定した回帰直線(赤い線)は、以下のように真の回帰直線とはズレたものとなってしまっています。
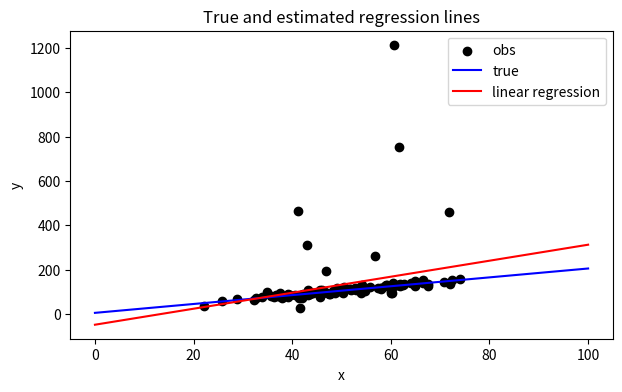
このように外れ値が存在する場合には、誤差項$\varepsilon_i$の分布にt分布やコーシー分布など正規分布よりも裾が厚い分布を用いることで、より外れ値に頑健な推定が可能になります。
誤差項を変えてみる
以下の密度関数をもつ確率変数$u$を考えます。(ただし、$\gamma>0$)
$$
f(u_i|\gamma) = \frac{\gamma}{1+u_i} \frac{1}{\{1+\log(1+u_i)\}^{1+\gamma}}
$$
また、潜在変数$z_i$、および0~1の値域をもつ確率変数$p$を以下のように定義します。
$$
Pr(z_i=1) = 1 – Pr(z_i=0) = p
$$
各$i$に対する潜在変数$z_i$の値によって、誤差項$\varepsilon_i$のしたがう分布を以下のように分けます。
$$
\varepsilon_i \sim
\begin{cases}
N(0, \sigma^2) & (z_i=0) \\
N(0, \sigma^2 u_i) & (z_i=1)
\end{cases}
$$
つまり、$z_i=0$の場合には観測値$i$は外れ値ではなく、誤差項は正規分布$N(0, \sigma^2)$にしたがいます。一方$z_i=1$の場合は観測値$i$は外れ値となり、その誤差項の分布は$N(0, \sigma^2u_i)$と、$z_i=0$の場合よりも分散が大きい分布となります。
このように定義された$\varepsilon_i$の分布を、論文中ではExtremely Heavily-tailed error分布(EH分布)と名付けています。このEH分布は、コーシー分布よりもさらに裾が厚いなど、外れ値に対してより頑健な性質を持ちます。(詳細は省略)
また、一見複雑そうな形式をしていますが、潜在変数を追加することでギブスサンプリングが可能になるため、MCMCも比較的簡単に実行できるという利点もあります。(こちらも詳細は省略)
さらにこのEH分布の副産物として、潜在変数$z_i$の事後分布を見ることで、各観測値$i$が外れ値である事後確率を計算可能であるというメリットもあります。
論文著者の1人である菅澤さんは、このEH分布に“自由度0のt分布”というキャッチーな別名称を使っていらっしゃいます。(ただし、論文中にはこの別名称は出てきません)
余談ですが、論文著者の御三方(羽村さん・入江さん・菅澤さん)はいずれも日本国内における統計学の第一人者で、特に入江さん・菅澤さんは昨年出版され話題になった『標準ベイズ統計学』の訳者でもあります。
Numpyroを使う上での課題
先ほど述べたように、EH分布はギブスサンプリングによるMCMCが可能ではあるのですが、とはいえ初学者やビジネスサイドの人たちにとってギブスサンプリングを一から実装するのは簡単ではありません。
(著者の1人である菅澤さんが、GithubにてRでのギブスサンプリングコードを公開してくれてはいます)
そこで今回は、確率的プログラミング言語(PPL)であるNumpyroを使った、EH分布による線形回帰分析を実装してみます。Numpyroであれば、ギブスサンプリングで必要な追加潜在変数や、条件つき確率分布の導出も必要ありません。
ただし、実はNumpyro(というかPPL)を使用することで生じてしまう課題が2つあります。まずはこれら課題とその解決方法をご紹介します。
課題1:離散潜在変数のサンプリング
1つ目の課題として、一般的にPPLでは連続変数のサンプリングはできますが、離散変数のサンプリングはできません。今回の例でいうと、外れ値かどうかを表す変数$z_i$は0 or 1のどちらかの値しかとらない離散変数のため、Numpyro含むPPLではそのままMCMCサンプリングすることは不可能です。
そこで、一度$z_i$は周辺化、つまり$z_i$を積分消去することでモデル式から$z_i$を消してしまい、$z_i$以外のパラメータをMCMCでサンプリングします。
その後、サンプリングしたパラメータおよび観測値$y_i$で条件づけた$z_i$の事後分布から$z_i$をサンプリングする、という2段階のアプローチをとります。
この周辺化ですが、Numpyroではモデルを定義する関数の前に@config_enumerateというデコレータをつけるだけで、勝手に内部で周辺化してくれます。(便利すぎる…!!)
課題2:EH分布の実装
もう1つの課題として、今回のモデルの肝であるEH分布の実装があります。当然ですが、このような全く新しい分布はNumpyroには搭載されていません。
ではどうするのかというと、既存の分布にしたがう確率変数に変数変換をかけまくり、EH分布にしたがう変数を作り出すことでこの課題を解決します。
まず、確率変数$Z$がパレート分布$Pareto(1, \gamma)$にしたがうとします。$Z$の確率密度関数$g(z)$は以下になります。(ただし、$Z>1$)
$$
g(z) = \frac{\gamma}{z^{\gamma+1}}
$$
この変数$Z$に対し、以下のような変換を施した変数を$U$とします。
$$
U = \exp(Z – 1) – 1
$$
このとき、$Z=1+\log(1+U)$となるので、ヤコビアンは$\left|\frac{d Z}{d U}\right| = \frac{1}{1+U}$となります。よって$U$の確率密度関数$f(u)$は、
$$
f(u) = g(z) \cdot \left|\frac{d Z}{d U}\right| = \frac{\gamma}{1+u} \frac{1} {\{1 + \log(1+u)\}^{1+\gamma}}
$$
となります。この式は、上述の$f(u_i|\gamma)$と全く同じ式になっていることがわかります。よって、パレート分布さえ定義できればEH分布も定義可能ということです。
Numpyroにはパレート分布は搭載されており、また確率変数の変数変換も簡単にできる機能がありますので、実装もとても簡単に行えます。これについては後述します。
以上、PPLを使う上で2つの課題がありはするが、Numpyroであれば簡単に解決可能であることを解説いたしました。
Numpyroでの実装
では、Numpyroで実装してみます。
まずは必要なライブラリのインポート。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import arviz as az
from tqdm import tqdm
import jax
import jax.numpy as jnp
import jax.random as random
import numpyro
import numpyro.distributions as dist
from numpyro.distributions.transforms import (
AffineTransform,
ExpTransform,
PowerTransform,
)
from numpyro.contrib.funsor import config_enumerate
from numpyro.infer import Predictive, init_to_median
from numpyro.infer import MCMC, NUTS
# MCMCを4chain並列に回すための設定
numpyro.set_host_device_count(4)今回使用するデータは、先ほど散布図を示した外れ値を含む以下ダミーデータです。
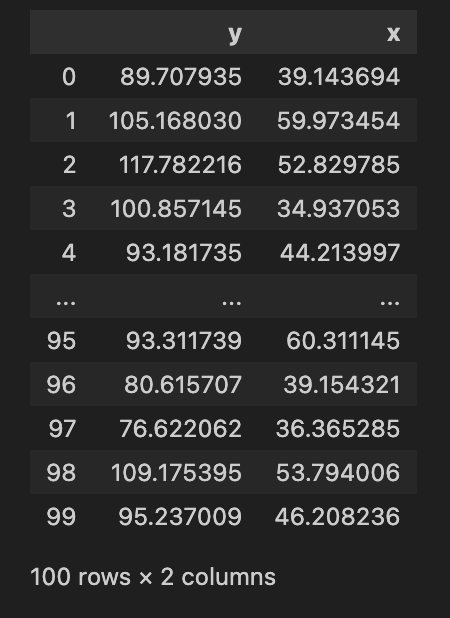
ではNumpyroでモデルを定義します。このモデルでは以下がミソになっています。
- モデルを定義する直前にデコレータ
@config_enumerateをつける (離散値に対して勝手に周辺化処理をしてくれる) uの事前分布には、前述の通りパレート分布に複数の変数変換をかけたものを定義
@config_enumerate
def model_ehe(y: jnp.array = None, x: jnp.array = None):
# 外れ値になる確率p(事前分布:ベータ分布)
p = numpyro.sample("p", dist.Beta(1, 4))
# EH分布内のパラメータgamma(事前分布:指数分布)
gamma = numpyro.sample("gamma", dist.Exponential(1))
# uの事前分布を定義
# パラメータgammaをもつパレート分布に対し、複数の変換を行う
u = numpyro.sample(
"u",
dist.TransformedDistribution(
base_distribution=dist.Pareto(1, gamma),
transforms=[
# 1を引き
AffineTransform(loc=-1, scale=1),
# 指数変換して
ExpTransform(),
# もう一度1を引く
AffineTransform(loc=-1, scale=1),
],
),
)
# 誤差項の標準偏差(外れ値でなければ1, 外れ値であればsqrt(u))
scale_eps = jnp.array([1.0, jnp.sqrt(u)])
# 全誤差項で共通の尺度sigmaは、逆ガンマ分布をベースにし平方根をとる
sigma = numpyro.sample(
"sigma",
dist.TransformedDistribution(
base_distribution=dist.InverseGamma(1, 1),
transforms=[PowerTransform(exponent=0.5)],
),
)
# 切片alphaの事前分布
alpha = numpyro.sample("alpha", dist.Normal(0, 10))
# 係数betaの事前分布
beta = numpyro.sample(
"beta",
dist.Normal(jnp.zeros(x.shape[1]), 10 * jnp.ones(x.shape[1])).to_event(1),
)
# 観測点ごとに繰り返し処理を行うためのplate構造
N = x.shape[0]
with numpyro.plate("data", N):
# 確率pのベルヌーイ分布から、外れ値フラグis_outlierをサンプリング
is_outlier = numpyro.sample("is_outlier", dist.Bernoulli(probs=p))
# 平均値muを計算
mu = numpyro.deterministic("mu", alpha + jnp.dot(x, beta))
# 正規分布に基づいて、観測値yをサンプリング
# スケールは外れ値かどうかで変える
y = numpyro.sample("y", dist.Normal(mu, sigma * scale_eps[is_outlier]), obs=y)このモデルにデータを投入し、MCMCを実行します。私の環境では8秒で終わりました。
rng_key = random.PRNGKey(123)
kernel = NUTS(model_ehe, init_strategy=init_to_median(num_samples=20))
# progress_bar=Falseにすると、計算スピードがアップするらしい
mcmc = MCMC(
kernel,
num_warmup=1000,
num_samples=4000,
thinning=1,
num_chains=4,
progress_bar=True,
)
mcmc.run(rng_key, y=jnp.array(df["y"]), x=jnp.array(df[["x"]]))MCMCの結果を取得します。
# MCMCサンプルを取得
mcmc_samples = mcmc.get_samples(group_by_chain=False)
# arvizでの可視化用
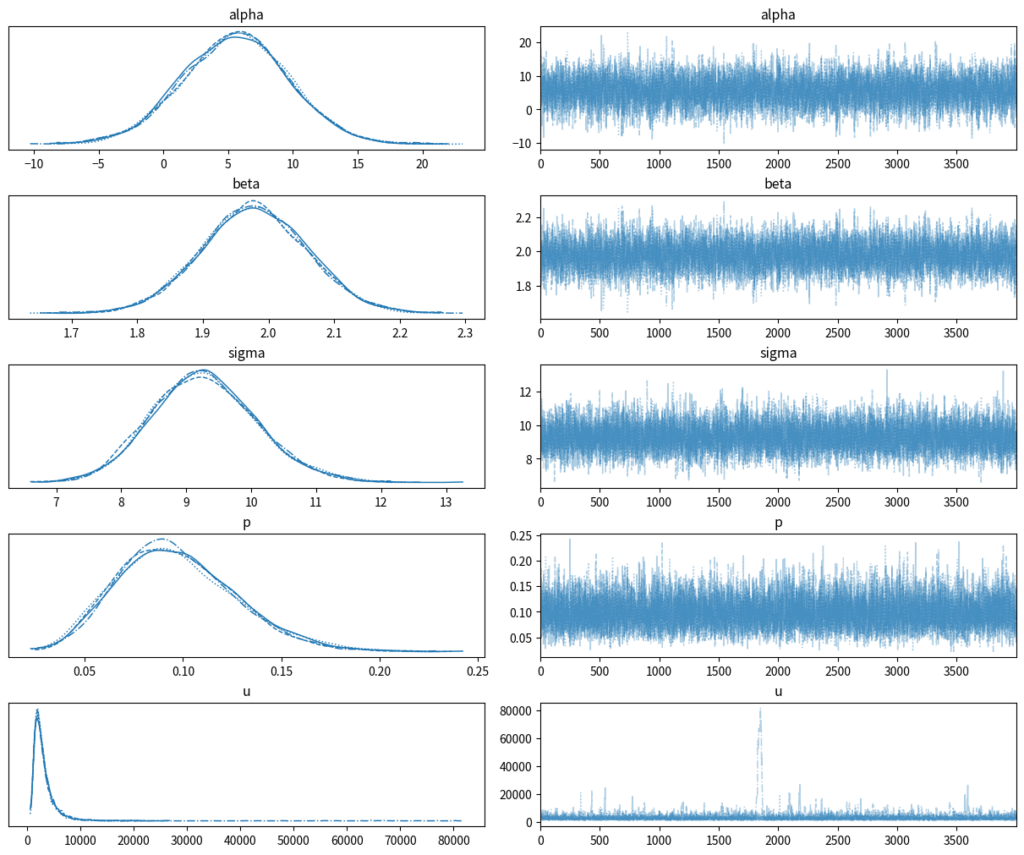
inference_data = az.from_dict(mcmc.get_samples(group_by_chain=True))トレースプロットを見てみると、収束も問題なさそうです。
az.plot_trace(
inference_data,
combined=False,
var_names=["alpha", "beta", "sigma", "p", "u"],
# グラフの文字が被らないようにする設定
# 参考:https://toeming.hatenablog.com/entry/2022/06/05/ArviZ_GetInShape
backend_kwargs={"constrained_layout": True},
)
次に、MCMCで生成した事後サンプルを使い、$y_i$の事後予測サンプルを生成します。その後、事後予測分布の平均および90%HDIを可視化してみます。すると、外れ値の点は漏れなくHDIの外側にあり、逆に外れ値でない点は回帰直線の上にあります。このことから、外れ値の影響を受けずに回帰直線を推定してくれていそうなことが分かります。
rng_key = random.PRNGKey(123)
# 説明変数xは0~100で等間隔に設定
x_pred = np.linspace(0, 100, 100)[:, np.newaxis]
# 目的変数yの事後予測サンプルを生成
predictive = Predictive(model_ehe, mcmc_samples)
prediction = predictive(rng_key, x=jnp.array(x_pred))["y"]
# 平均および90%HDIをまとめたデータフレームを作成
y_predictive_mean = np.mean(prediction, axis=0)
y_predictive_hdi = az.hdi(np.array(prediction)[np.newaxis, :, :], hdi_prob=0.9)
df_prediction = pd.DataFrame(
{
"mean": y_predictive_mean,
"lwr": y_predictive_hdi[:, 0],
"upr": y_predictive_hdi[:, 1],
}
)
# 事後予測分布を可視化
fig, ax = plt.subplots(figsize=(7, 4))
ax.scatter(df["x"], df["y"], color="black", label="obs")
ax.plot(x_pred[:, 0], df_prediction["mean"], color="blue", label="mean")
ax.fill_between(
x_pred[:, 0],
df_prediction["lwr"],
df_prediction["upr"],
color="blue",
alpha=0.2,
label="interval",
)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Posterior predictive distribution", loc="left")
ax.legend()
fig.show()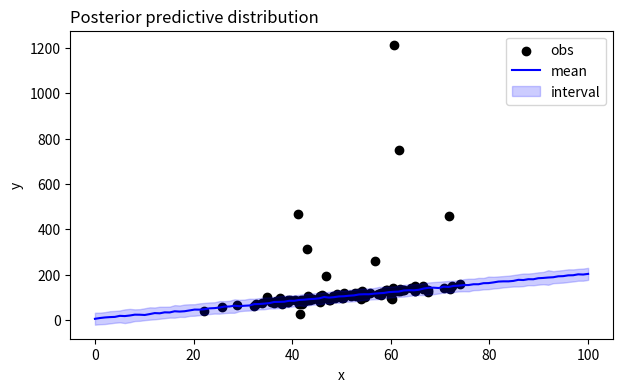
続いて、各観測値が外れ値である事後確率を求めてみます。先ほど$y_i$の事後サンプルを生成したのと同様に、MCMCサンプルとデータを与えてあることで、外れ値かどうかのインデックス$z_i$の事後サンプルが生成できます。
ただし、Predictive関数に引数としてinfer_discrete=Trueを与えてあげる必要があります。この引数を設定することで、MCMCのときには周辺化して無視した離散値$z_i$の事後サンプルを生成できます。
rng_key = random.PRNGKey(123)
# 離散値z_iの事後サンプルを生成
predictive_discrete = Predictive(model_ehe, mcmc_samples, infer_discrete=True)
prediction_discrete = predictive_discrete(
rng_key, y=jnp.array(df["y"]), x=jnp.array(df[["x"]])
)このようにして生成した$z_i$事後サンプルをもとに各$i$に対する平均を計算し、これを”$i$が外れ値になる事後確率”と扱うことにします。そして、この”外れ値になる事後確率”が0.9より大きい$i$を外れ値と定義し、散布図で色分けして可視化してみます。
すると、外れ値であるデータをきちんと”外れ値”として推定してくれていることが分かります。
# z_iの事後平均を計算 -> 各観測値が外れ値になる事後確率とする
outlier_prob = np.mean(prediction_discrete["is_outlier"], axis=0)
df_outlier_flg = df.copy()
# 外れ値の事後確率が0.9より大きい観測値を"外れ値"と定義する
df_outlier_flg["outlier_status"] = [
"outlier" if p > 0.9 else "standard" for p in outlier_prob
]
# 散布図を"外れ値"か"通常"かで色分け
fig, ax = plt.subplots(figsize=(7, 4))
sns.scatterplot(data=df_outlier_flg, x="x", y="y", hue="outlier_status", ax=ax)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend()
fig.show()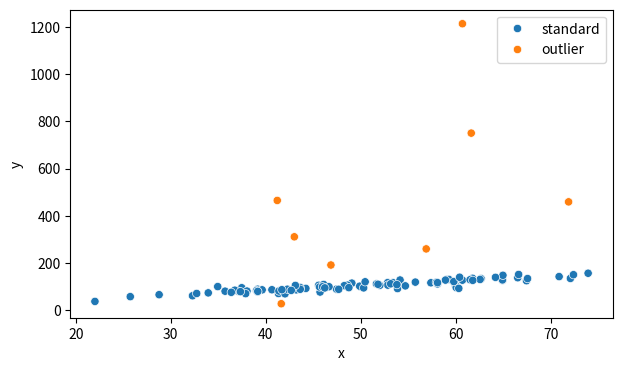
外れ値の割合による影響
ここまでは、グラフで可視化しやすいように説明変数が1次元しかない例を扱ってきました。が、実際は説明変数が1次元であるケースは少ないと思うので、もうちょっと一般化して、説明変数が5次元のダミーデータを使ってみます。
$$
y_i = \alpha + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \beta_4x_4 + \beta_5x_5 + \varepsilon_i
$$
さらに、外れ値が発生する割合を0.05, 0.1, 0.2, 0.3の4パターンで試してみて、外れ値の割合が変わると推定結果がどう変わるかも一緒に見てみました。
さらにさらに、普通の線形回帰(=誤差項が正規分布)のモデルと比較して、結果にどんな差異が出るかも見てみます。
結果が以下です。横軸が外れ値の割合、点線が真の係数の値です。これを見ると、
- 普通の線形回帰(
normal)よりも、EHE分布を使ったモデル(EHE)のほうが係数の信用区間が狭く、かつ真の値(点線)がちゃんと区間内に入る傾向にある - 普通の線形回帰は、外れ値の割合が高くなるほど信用区間が広くなってしまう。一方EHEモデルによる推定結果は、外れ値の割合の影響をほとんど受けていない
ということが分かります。
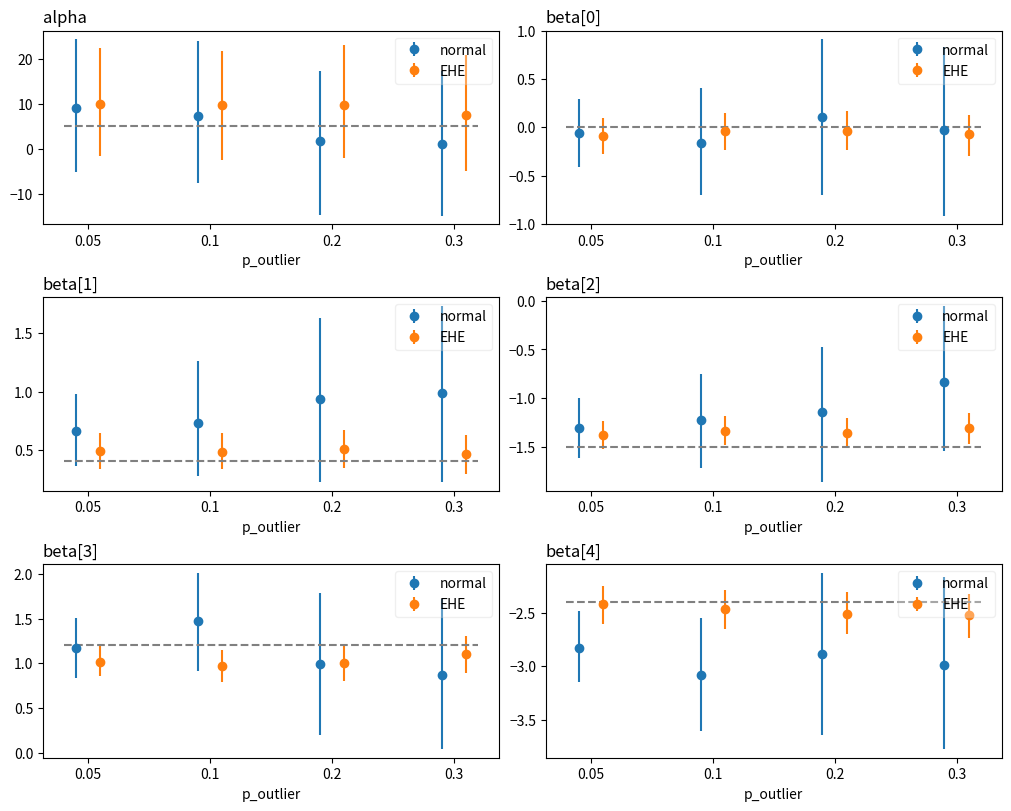
この実験結果を見る限りでは、外れ値を含むデータに対しては、EHE分布を使った線形回帰は強力なアプローチと言えそうです。
まとめ
今回は、外れ値に強い”自由度0のt分布”を使った回帰分析をNumpyroで実装してみました。個人的には、”自由度0のt分布”という手法についても大変勉強になったのですが、Numpyroの便利な機能(離散変数の周辺化・変数変換)についても知ることができて良かったです。
機会があれば、この離散変数の周辺化機能を使ったspike and slab priorの実装にもチャレンジしてみようと思います。
参考
- 論文:『Log-Regularly Varying Scale Mixture of Normals for Robust Regression』
- 論文著者の菅澤さんによるQiita解説記事:
- HELLO CYBERNETICS:『NumPyroの基本を変化点検知で見る』
- Zenn記事:『NumPyro:離散潜在変数の扱い方』