Python用のライブラリであり、確率的プログラミング言語(PPL)のひとつでもあるPyMCには、実験的な機能や十分にテストしきれていない機能を提供するpymc-experimentalという派生ライブラリが存在します。
このpymc-experimentalですが、線形ガウス状態空間モデルを簡単に実行できるモジュールが含まれていたため、今回の記事ではpymc-experimentalを使って状態空間モデルを実行する方法をご紹介していきます。
注意:pymc-experimentalは上述の通り実験的な機能を集約したライブラリのため、バグが潜んでいる可能性も大いにあります。また今回紹介するモジュールが今後正式にPyMCに収録された際には、関数名やその使用方法が変更されることもあり得るので、その点ご了承ください。
ちなみに、別のPython用PPLであるNumpyroを使った状態空間モデルの実装についても過去記事で紹介していますで、よければそちらもご覧ください。
使用データ
今回もいつも通りGoogle Trendsのデータを使います。『引越し』というワードの検索数データをGoogle Trendsのサイトからcsv形式でダウンロードしておきます。単位は週次(7日間ごとの値)です。
(注:下図のグラフは5年間くらいのデータのうち、直近約2年半のものです。最大値が100になっていないのはそのためです。)
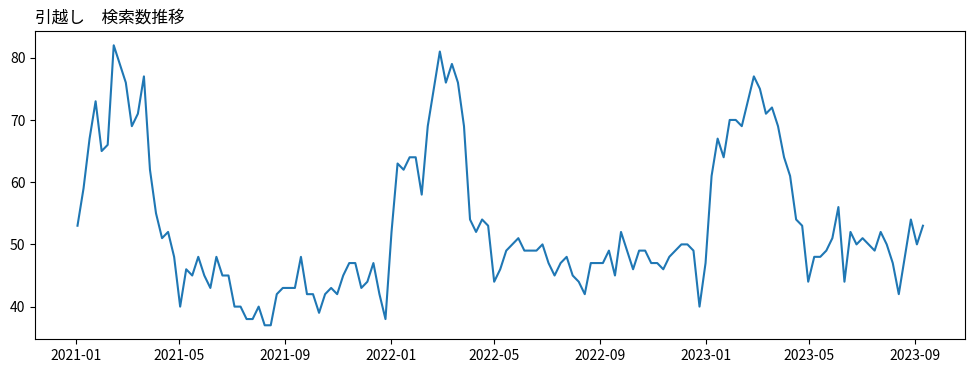
今回”引越し”というワードを使用した理由は、顕著な季節性が存在すると考えたためです。グラフを見ると、毎年1月〜4月に検索数が増える傾向にあります。理由は明らかで、この時期は4月の新生活前に引越しを検討する人がたくさんいるためだと思われます。
モデル
このデータに状態空間モデルを適用し、トレンド成分と周期性成分に分解してみようと思います。
$$
y_t = \mu_t + \gamma_t + \varepsilon_t,\ \varepsilon_t \sim N(0, \sigma^2)
$$
各項は以下を表します。
- $\mu_t$:トレンド項
- $\gamma_t$:季節性項
- $\varepsilon_t$:誤差項
$\mu_t$は以下のように時間変動させます。
$$
\begin{cases}
\mu_t = \mu_{t-1} + \delta_{t-1} + \eta_t,\quad \eta_t \sim N(0, \sigma_\eta^2) \\
\delta_t = \delta_{t-1} + \xi_t, \quad \xi_t \sim N(0, \sigma_\xi^2)
\end{cases}
$$
上式はローカル線形トレンドモデルそのもので、$\delta_t$はトレンド項の傾きを表します。
季節性の成分$\gamma_t$については、以下のように構成されます。
$$
\gamma_t = \sum_{n=1}^N \gamma_{n, t}
$$
各$\gamma_{n, t}$は、以下の式にしたがって時間変動します。(なぜこのような式になるのかについては、書籍『基礎からわかる時系列分析』を参照ください)
$$
\begin{gather}
\begin{cases}
\gamma_{n, t} = \gamma_{n, t-1}\cos \lambda_{n} + \gamma_{n, t-1}^\ast \sin \lambda_{n} +\omega_{n, t} \\
\gamma_{n, t}^\ast = -\gamma_{n, t-1}\sin \lambda_{n} + \gamma_{n, t-1}^\ast \cos \lambda_{n} + \omega_{n, t}^\ast
\end{cases}
\end{gather}
$$
ただし、$\lambda_{n} = \frac{2\pi n}{S}$とし、$S$は時系列データの周期とします。今回だと週次データを使うので、$S=52$となります。(1年=52週間)
上式を行列形式で表すと、以下のようになります。こっちのほうがスッキリして見やすいかなと思います。
$$
\pmatrix{\gamma_{n, t} \\ \gamma_{n, t}^\ast} = \pmatrix{\cos \lambda_n & \sin \lambda_n \\ -\sin \lambda_n & \cos \lambda_n } \pmatrix{\gamma_{n, t-1} \\ \gamma_{n, t-1}^\ast} + \pmatrix{\omega_{n, t} \\ \omega_{n, t}^\ast}
$$
後ろにくっついている$\omega_{n,t}, \ \omega_{n,t}^\ast$は、正規分布にしたがう確率変数です。もしこの項がなければ、$\gamma_{n,t}$および$\gamma_t$は、同じ季節であれば全く同じ値をとります。しかし正規分布にしたがう変数を加えることで値が変化できるようになるため、季節成分の値が変化することを許容したモデルになります。
一般的には、$\omega_{1,t}, \omega_{1,t}^\ast, \dots, \omega_{n, t},\omega_{n, t}^\ast, \dots, \omega_{N,t}, \omega_{N, t}^\ast$はそれぞれ異なる正規分布にしたがう、としてもよいのですが、pymc-experimentalでは簡単のために全て同じ正規分布$N(0, \sigma_\omega^2)$に独立にしたがうとしたモデルのみ取り扱えるようです。(ここもライブラリのバージョンによって今後変わってくるかもしれません)
また$N$の値についてはハイパーパラメータで、ここの値を大きくすればするほど複雑な周期性の波を表現できるようになります。今回のような週次データの場合、私の経験則だと$N$は2~5くらいに収まることが多いです。
実装
では実装してみます。基本的にはこちらのPyMCの掲示板に投稿されている記事を参考にしていますので、こちらもご参照ください。
ちなみに主要なライブラリのバージョンは以下で実行しました。
- PyMC : 5.7.2
- pymc-experimental : 0.0.11
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pymc as pm
import pymc_experimental.statespace.models.structural as st
import pytensor.tensor as pt
import arviz as azpandasのデータフレームでデータを読み込みます。日付を表す列はindexに設定しておきます。
# データ読み込み
df = pd.read_csv(
"ファイルパス",
skiprows=2,
index_col="週",
parse_dates=True,
)
df = df.rename(columns={"引越し: (日本)": "value"})
# indexの設定
df.index.name = "week"
df.index.freq = "W"
# 型変換
df["value"] = df["value"].astype(float)
# 日付でフィルタ
df = df[df.index >= "2021-01-01"]ではpymc-experimentalでの状態空間モデルまわりの設定を行います。といってもモデル構築自体はとても簡単で、以下のように要素ごとに定義し、最後に全て足し合わせてbuildするだけです。ちなみに季節性のハイパーパラメータ$N$の値は5にしてみました。
# Level成分(order=2でローカル線形トレンドモデル)
ll = st.LevelTrendComponent(order=2)
# seasonality(次数5のフーリエ級数)
se = st.FrequencySeasonality(
season_length=52,
n=5,
name="weekly",
)
# 観測誤差
er = st.MeasurementError()
mod = ll + se + er
ss_mod = mod.build()buildすると以下のメッセージが表示されます。これは、各種パラメータの名称や次元数をご丁寧に教えてくれています。
The following parameters should be assigned priors inside a PyMC model block:
initial_trend -- shape: (2,), constraints: None, dims: ('trend_state',)
sigma_trend -- shape: (2,), constraints: Positive, dims: ('trend_shock',)
weekly -- shape: (10,), constraints: None, dims: (weekly_initial_state, )
sigma_weekly -- shape: (1,), constraints: Positive, dims: None
sigma_MeasurementError -- shape: (1,), constraints: Positive, dims: None
P0 -- shape: (12, 12), constraints: Positive semi-definite, dims: ('state', 'state_aux')
ではこれで設定は終わりかというとそうではなく、上記メッセージで表示されている各種パラメータに事前分布を設定する必要があります。
今回取り扱っているのは線形ガウス状態空間モデルですので、各種パラメータの値が決まれば、カルマンフィルタおよび平滑化を利用することで、状態変数の事後分布は解析的に得られます。
今回のモデルでいうと、各分散パラメータ($\sigma^2, \sigma_\eta^2, \sigma_\xi^2, \sigma_\omega^2$)や各状態変数の$t=0$における初期値($\mu_0, \delta_0, \omega_{1,0},\omega_{1,0}^\ast, \dots, \omega_{N, 0}, \omega_{N, 0}^\ast$)の値が決まれば、$\mu_t, \delta_t, \omega_{1,t}, \dots, \omega_{N,t}$($t=1,\dots,T$)の事後分布、つまり$y_1,\dots,y_T$を所与とした分布$p(\cdot | y_1,\dots,y_T)$はすべて正規分布になり、かつその平均・分散の値はカルマンフィルタ+平滑化によって明示的に求められます。(ごちゃごちゃした行列計算は必要ではありますが)
また、各種パラメータ(1個1個表記するのがめんどくさいので、まとめて$\Theta$と置きます)の値が決まれば、上記のカルマンフィルタ実行中に副産物として求まる数値を流用することで、対数尤度$\log p(y_{1:T}|\Theta)$の値も求めることができます。そのため、事前分布$p(\Theta)$を与えれば、以下の$\Theta$の事後分布
$$
p(\Theta|y_{1:T}) \propto p(y_{1:T}|\Theta) p(\Theta)
$$
をMCMC等で計算可能ということになります。もしくは最尤法により、$p(y_{1:T}|\Theta)$を最大にする$\Theta$を求めるというアプローチも可能です。いずれにせよ、状態変数の値は必要ではないことに注意してください。
対数尤度$\log p(y_{1:T}|\Theta)$の値を求める方法については、本記事の最後で補足として記載していますので、興味のある方はご覧ください。
カルマンフィルタと平滑化については以前ブログで紹介しましたので、ぜひそちらもご参照ください。
よって、pymc-experimentalでは以下のステップで各種パラメータおよび状態変数の事後分布を求めています。
- 各種パラメータ$\Theta$に事前分布を設定し、MCMCによって$\Theta$の事後分布からのサンプルを得る
- 1で得たサンプル1つ1つに対し、カルマンフィルタ+平滑化を実行し、状態変数の事後分布の平均・分散を算出する
- 2で計算した平均・分散をもとに、状態変数の事後正規分布からのサンプルを生成する
ということで上記1を実行します。普通のPyMCで行うのと同様のモデル記述を行えばOKです。唯一気をつけないといけない点は、各種パラメータの名称および次元数を、先ほどモデルをbuildした際に表示されたメッセージと揃えないといけない点です。
with pm.Model(coords=ss_mod.coords) as model:
# 初期値の分散
P0_diag = pm.Gamma("P0_diag", alpha=2, beta=1, dims=["state"])
P0 = pm.Deterministic("P0", pt.diag(P0_diag), dims=["state", "state_aux"])
# 初期値
initial_trend = pm.Normal("initial_trend", sigma=100, dims=["trend_state"])
weekly = pm.Normal("weekly", sigma=10, dims=["weekly_initial_state"])
# 状態変数の分散
sigma_trend = pm.Gamma("sigma_trend", alpha=5, beta=1, dims=["trend_shock"])
sigma_weekly = pm.Gamma("sigma_weekly", alpha=2, beta=1)
sigma_measurementerror = pm.Gamma("sigma_MeasurementError", alpha=10, beta=1)
ss_mod.build_statespace_graph(data=df)各パラメータの依存関係をパス図で表現してみます。ごちゃごちゃしていて一見何が何だか分かりませんが、よくよく見てみると、状態変数(〇〇_state)から観測値(obs)には矢印は伸びていないことが分かります。
pm.model_to_graphviz(model)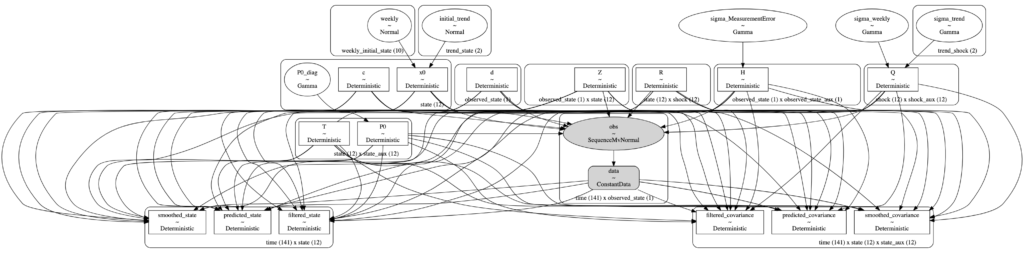
ではMCMCを実行します。バーンイン回数は1,000、その後の事後サンプルサイズを2,000、チェイン数は4としています。
with model:
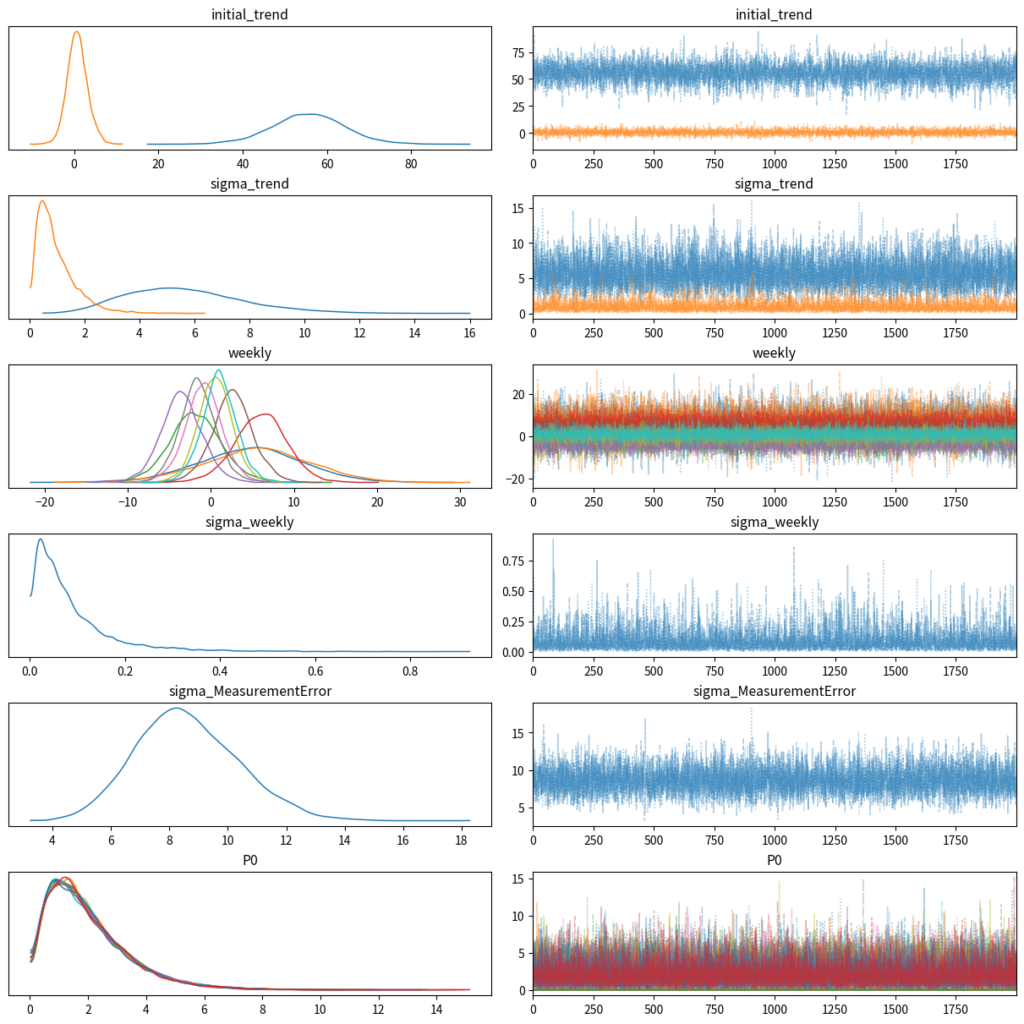
idata = pm.sample(draws=2000, tune=1000, random_seed=123, cores=4)事後サンプルのチェックをします。収束状況は問題なさそうです。
az.plot_trace(
idata,
combined=True,
var_names=ss_mod.param_names,
# グラフの文字が被らないようにする設定
# 参考:https://toeming.hatenablog.com/entry/2022/06/05/ArviZ_GetInShape
backend_kwargs={"constrained_layout": True},
)
続いて、各パラメータのMCMCサンプルをもとに、状態変数の事後サンプルを生成します。
# 状態変数の事後サンプリングを実行
post = ss_mod.sample_conditional_posterior(idata, random_seed=123)続いて、状態変数の事後サンプルをもとに、モデル内の各要素$\mu_t, \delta_t, \gamma_t$の値を算出します。例えば周期性だと、各状態変数$\gamma_{1,t},\gamma_{2,t},\dots,\gamma_{n,t}$の事後サンプルは得られているので、これらをもとに$\gamma_t = \sum_{n=1}^N \gamma_{n, t}$の計算によって、$\gamma_t$の事後サンプルを取得します。
# 状態変数の事後サンプルをもとに、トレンドや周期性などの要素を算出
component_idata = ss_mod.extract_components_from_idata(post)
# 各要素の名前を取得
component_states = component_idata.coords["state"].values.tolist()
component_state各要素の事後平均と95%HDI区間を可視化してみます。weeklyを見ると、毎年1月~4月に検索数が増える特徴を捉えられていますね。
fig, axis = plt.subplots(3, 1, figsize=(10, 6), constrained_layout=True)
axis = axis.flatten()
for name, ax in zip(component_states, axis):
data = component_idata.smoothed_posterior.sel(state=name)
# 95%HDI区間
hdi = az.hdi(data, hdi_prob=0.95).smoothed_posterior.values
lwr = hdi[:, 0]
upr = hdi[:, 1]
# 事後平均
mean = data.mean(dim=["chain", "draw"])
ax.plot(df.index, mean)
ax.fill_between(df.index, y1=lwr, y2=upr, color="tab:blue", alpha=0.1)
ax.set_title(name)
plt.show()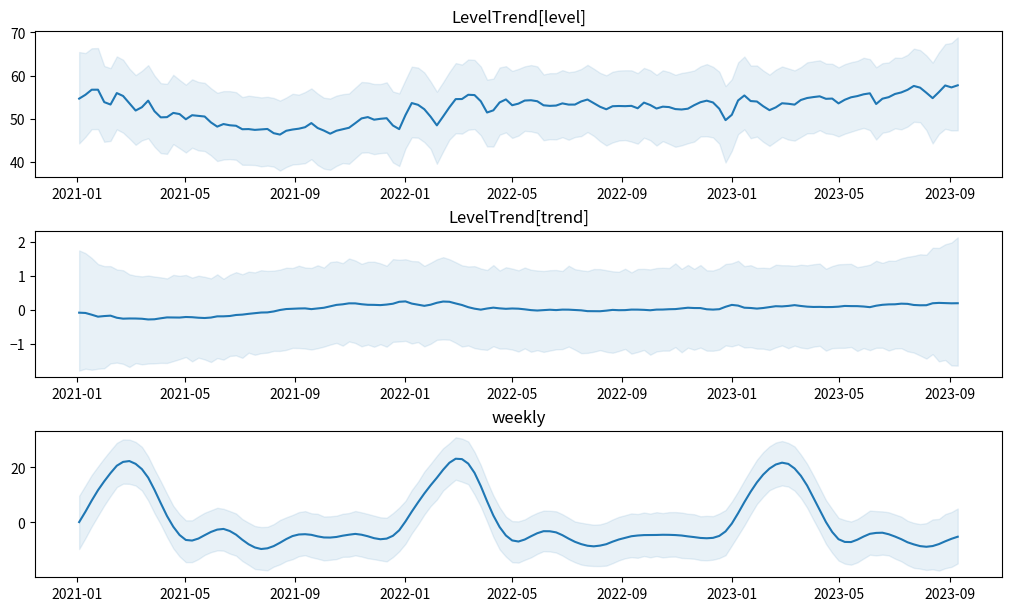
さらに、目的変数の予測値$\hat{y_t}$の事後分布も可視化してみます。元データの推移を大分追えているかなと思います。
fig, ax = plt.subplots(figsize=(10, 4))
post_stacked = post.stack(sample=["chain", "draw"])
hdi_post = az.hdi(post, hdi_prob=0.95).smoothed_posterior_observed.squeeze().values
lwr_post = hdi_post[:, 0]
upr_post = hdi_post[:, 1]
ax.scatter(df.index, df["value"], label="Data", color="k", s=10)
ax.plot(
df.index,
post_stacked.smoothed_posterior_observed.squeeze().values.mean(axis=1),
label="Posterior",
)
ax.fill_between(df.index, y1=lwr_post, y2=upr_post, alpha=0.3, label="HDI")
ax.legend()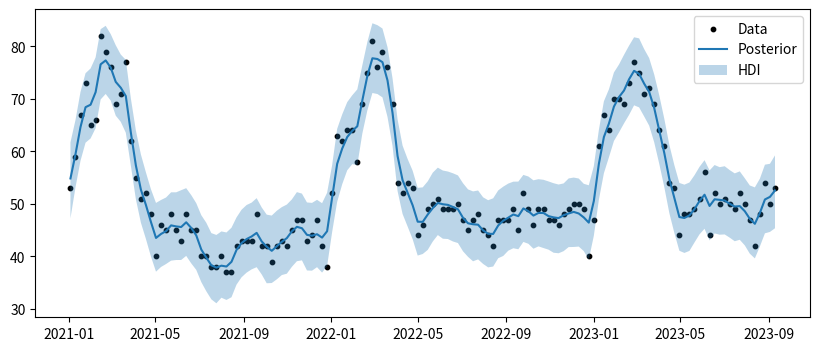
ついでに将来予測もやってみます。pymc-experimentalなら将来予測も簡単に実行できました。予測期間は52週(1年後まで)としました。
# 将来予測値のサンプルを生成
forecasts = ss_mod.forecast(idata, start=df.index[-1], periods=52)
forecasts_stacked = forecasts.stack(sample=["chain", "draw"])
hdi_forecasts = az.hdi(forecasts, hdi_prob=0.95).forecast_observed.squeeze().values
lwr_forecasts = hdi_forecasts[:, 0]
upr_forecasts = hdi_forecasts[:, 1]将来予測も併せて可視化してみます。オレンジの区間が右に行くにつれてかなり広くなってしまっていますが、これは$\mu_t, \delta_t, \gamma_t$の3つの要素の不確実性は、時間が進むにつれて累積していくためです。
fig, ax = plt.subplots(figsize=(10, 5))
# 観測値
ax.scatter(df.index, df["value"], label="Data", color="k", s=10)
# 学習期間
ax.plot(
df.index,
post_stacked.smoothed_posterior_observed.squeeze().values.mean(axis=1),
label="Posterior",
)
ax.fill_between(df.index, y1=lwr_post, y2=upr_post, alpha=0.25, label="HDI")
# 将来期間
ax.plot(
forecasts.coords["time"],
forecasts_stacked.forecast_observed.squeeze().values.mean(axis=1),
alpha=1,
label="Mean Posterior Forecast",
)
ax.fill_between(
forecasts.coords["time"],
y1=lwr_forecasts,
y2=upr_forecasts,
alpha=0.25,
label="Forecast HDI",
)
ax.legend()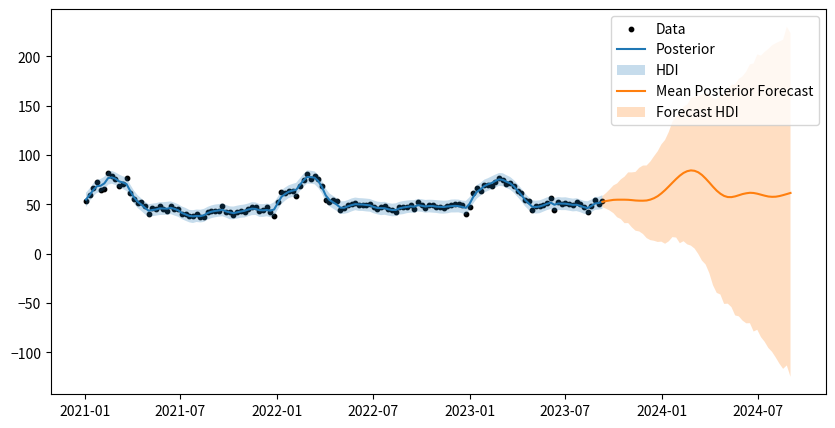
実装についてはこれで終わりです。
まとめ
本記事では、PyMCの実験機能を集めたライブラリpymc-experimentalによる、線形ガウス状態空間モデルの実装方法について取り上げました。
現状は別ライブラリですが、今後この機能は本家であるPyMCに取り込まれるはずですので、そうなるとPyMCの利便性がますます向上するでしょうね。
一方で、非線形・非ガウスの状態空間については非対応ですので、カスタマイズ性は高くはないのかなーと思いました。柔軟にカスタマイズしたい場合はPyMCのモデルを1から自分で書くしかないですが、それができる人はそもそも線形ガウスも自分で書けると思いますので、そのような人にはこの機能の需要はあまりないかもしれません。
また、例えば説明変数を入れたモデルなど、(線形ガウスの枠組みの中で)より一般的なモデルを扱うことができるのかな?というのも疑問に持ちました。公式ドキュメントをざっと見た感じ可能そうな雰囲気はありますが、今回はそこまでは調べられていません。機会があればそこまで調べてみようと思います。
補足:カルマンフィルタによる対数尤度の計算方法
パラメータ$\Theta$を所与とした対数尤度$\log p(y_{1:T}|\Theta)$は、以下のように書き換えることができます。
$$
\log p(y_{1:T}|\Theta) = \sum_{t=1}^T \log p(y_t|y_{1:t-1}, \Theta)
$$
上式から、各$t$に対する$\log p(y_t|y_{1:t-1}, \Theta)$を求められれば、それを足し合わせることで対数尤度が計算できることが分かります。今回は線形ガウス状態空間モデルを考えているので、$p(y_t|y_{1:t-1}, \Theta)$は正規分布になります。よって、$y_t|y_{1:t-1}, \Theta$の平均・分散が求まれば自動的に尤度が計算できることになります。
以降の計算では、カルマンフィルタのアルゴリズムの知識および表記を使いますので、こちらの記事と併せてご覧ください。
では、平均・分散を考えてみます。状態空間モデルを以下の式で定義します。$z_t$が状態変数、$y_t$が観測値です。
(注:以降の式はすべて$\Theta$は所与とし、式中からは記載を省略します。記載がめんどくさいので…)
$$
\begin{gather}
\begin{cases}
z_t = A z_{t-1} + \varepsilon_t \\
y_t = C z_t + \eta_t
\end{cases}\\
\varepsilon_t \sim N(0, Q) \\
\eta_t \sim N(0, R)
\end{gather}
$$
このとき、$y_t|y_{1:t-1}$の平均は以下のようになります。
$$
E[y_t|y_{1:t-1}] = \hat{y_t}=C \mu_{t|t-1}
$$
ただし、$\mu_{t|t-1}=E[z_t|y_{1:t-1}]$であり、これはカルマンフィルタの予測ステップにて計算される値です。つまり、カルマンフィルタを実行すれば、ついでに$C \mu_{t|t-1}$の値も計算可能です。
次に分散ですが、カルマンフィルタの計算途中で以下の値が出てきます。
$$
S_t = Cov[r_t|y_{1:t-1}] = C\Sigma_{t|t-1}C^T + R
$$
ただし、$r_t = y_t – \hat{y_t}$、$\Sigma_{t|t-1}=Cov[z_t|y_{1:t-1}]$です。$\Sigma_{t|t-1}$もカルマンフィルタの予測ステップで計算される値です。
ここで、$\hat{y_t}=C \mu_{t|t-1}$で定数ですので、$y_t$とそこから定数を引いた$r_t$は同じ分散になります。つまり$Cov[r_t|y_{1:t-1}]=Cov[y_t|y_{1:t-1}]$です。よって、$Cov[y_t|y_{1:t-1}]=S_t$となることがわかりました。
まとめると、$y_t|y_{1:t-1} \sim N(C \mu_{t|t-1}, S_t)$となります。これで各$t$における$\log p(y_t|y_{1:t-1}, \Theta)$が計算でき、結果$\log p(y_{1:T}|\Theta) = \sum_{t=1}^T \log p(y_t|y_{1:t-1}, \Theta)$も計算できることになります。