状態空間モデルの推論アルゴリズム(カルマンフィルタ・平滑化)

時系列データのモデリングとして代表的なものに、状態空間モデルがあります。状態空間モデルの特徴として、

• 定常性がないデータに適用可能
• 結果の解釈が容易
• 周期性や外部変数を組み込むなどの柔軟なカスタマイズができる

が挙げられます。

今回は、状態空間モデルの中でも一番オーソドックスな線形ガウス状態空間モデルと、その推論に使われるアルゴリズムをご紹介します。

線形ガウス状態空間モデル

本記事では、線形ガウス状態空間モデルを以下の数式で定義します。($t=1,\dots,T$とする)

$$
\begin{gather}
\begin{cases}
\boldsymbol{z_t} &= \mathbf{A}\boldsymbol{z_{t-1}} + \boldsymbol{\varepsilon_t} \\
\boldsymbol{y_t} &= \mathbf{C}\boldsymbol{z_t} + \boldsymbol{\delta_t}
\end{cases}, \\
\boldsymbol{\varepsilon_t} \sim N(\boldsymbol{0}, \mathbf{Q}), \\
\boldsymbol{\delta_t} \sim N(\boldsymbol{0}, \mathbf{R})
\end{gather}
$$

1つ目の式を状態方程式、2つ目の式を観測方程式といいます。

$\boldsymbol{z_t}$は目に見えない変数(潜在変数)で、実際に観測されることはありません。観測されるのは$\boldsymbol{y_t}$だけで、$\boldsymbol{z_t}$をもとに生成されます。また$\boldsymbol{z_t}$は一期前の自身の値$\boldsymbol{z_{t-1}}$から生成されてます。この構造によって、時系列データの前後に存在する依存関係を表現しています。

この式を見ると、

• $\boldsymbol{z_{t-1}}\rightarrow\boldsymbol{z_t}$、$\boldsymbol{z_t}\rightarrow\boldsymbol{y_t}$の式中に線形式しか出てこない
• $\boldsymbol{\varepsilon_t},\boldsymbol{\delta_t}$はともに正規分布

となっています。これが”線形ガウス”という名前の所以です。

線形ガウス状態空間モデルを時系列データに適用するには、観測値$\boldsymbol{y_t}$から潜在変数$\boldsymbol{z_t}$を推測する必要があります。ここでいう”推測”とは、「$\boldsymbol{z_t}$の値をただ一つ求める」ではなく、「$\boldsymbol{z_t}$の分布を求める」ことを意味しています。

線形ガウス状態空間モデルでは、そのシンプルさゆえに$\boldsymbol{z_t}$の分布(=正規分布の平均・分散の値)を陽に求めることができます。これがもっと複雑なモデル(非線形にする・正規分布以外を使うなど)になると、MCMCなどのアルゴリズムが必要になります。

$\boldsymbol{z_t}$の分布の種類

“$\boldsymbol{z_t}$の分布”と一口に言っても、条件づける観測値によって以下のように3種類に分けられます。

1. $\boldsymbol{z_t}|\boldsymbol{y_{1:t}}$：観測値$\boldsymbol{y_1},\dots,\boldsymbol{y_t}$の情報をもとにした、同時点の$\boldsymbol{z_t}$の分布
2. $\boldsymbol{z_t}|\boldsymbol{y_{1:T}}$：すべての観測値$\boldsymbol{y_1},\dots,\boldsymbol{y_T}$の情報をもとにした、$T$以前のとある時点$\boldsymbol{z_t}$の分布
3. $\boldsymbol{z_{T+k}}|\boldsymbol{y_{1:T}}$：すべての観測値$\boldsymbol{y_1},\dots,\boldsymbol{y_T}$の情報をもとにした、将来時点の$\boldsymbol{z_{T+k}}$の分布

1を実施するアルゴリズムをカルマンフィルタ、2を実施するアルゴリズムを平滑化(またはカルマンスムーザ)といいます。このアルゴリズムの詳細について以下で解説します。

ちなみに3の将来予測ですが、1のカルマンフィルタが実施できれば容易に実施できるので、今回は省略します。

注意：本記事では、その他のパラメータ($\mathbf{A},\mathbf{C},\mathbf{Q},\mathbf{R}$)の値は既知として扱いますが、実際はこれらの値もデータから推測する必要があります。これらの求め方については今回は省略します。

カルマンフィルタ

まずはカルマンフィルタを解説します。カルマンフィルタでは、以下式の$\boldsymbol{\mu_t},\mathbf{\Sigma_t}$を求めることが目的です。

$$
\boldsymbol{z_t}|\boldsymbol{y_{1:t}} \sim N(\boldsymbol{\mu_t}, \mathbf{\Sigma_t})
$$

カルマンフィルタは$t$を1つずつ増やして逐次的に実行していくので、1期前までのカルマンフィルタは実行済み(すなわち、$\boldsymbol{\mu_{t-1}},\mathbf{\Sigma_{t-1}}$の値は算出済み)とします。

予測ステップ

$\boldsymbol{z_t}|\boldsymbol{y_{1:t}}$の密度関数は、以下のように2つのブロックに分解することができます。

$$
p(\boldsymbol{z_t}|\boldsymbol{y_{1:t}}) \propto p(\boldsymbol{y_t}|\boldsymbol{z_t})p(\boldsymbol{z_t}|\boldsymbol{y_{1:t-1}})
$$

上式を使うために、$p(\boldsymbol{z_t}|\boldsymbol{y_{1:t-1}})$の分布を求めます。これは状態方程式$\boldsymbol{z_t} = \mathbf{A}\boldsymbol{z_{t-1}} + \boldsymbol{\varepsilon_t}$から、

$$
\begin{align}
\boldsymbol{\mu_{t|t-1}} \stackrel{\rm{def}}{=} E[\boldsymbol{z_t}|\boldsymbol{y_{1:t-1}}] &= \mathbf{A}E[\boldsymbol{z_{t-1}}|\boldsymbol{y_{1:t-1}}] \\
&= \mathbf{A}\boldsymbol{\mu_{t-1}}, \\
\mathbf{\Sigma_{t|t-1}} \stackrel{\rm{def}}{=} Var[\boldsymbol{z_t}|\boldsymbol{y_{1:t-1}}] &= \mathbf{A}Var[\boldsymbol{z_{t-1}}|\boldsymbol{y_{1:t-1}}]\mathbf{A}^T + Var[\varepsilon_t] \\
&= \mathbf{A\Sigma_{t-1}A}^T + \mathbf{Q}
\end{align}
$$

とすぐに求められます。

観測ステップ

次に、$p(\boldsymbol{z_t}|\boldsymbol{y_{1:t}}) \propto p(\boldsymbol{y_t}|\boldsymbol{z_t})p(\boldsymbol{z_t}|\boldsymbol{y_{1:t-1}})$を適用します。

これは、以前投稿したこちらの記事の結果がそのまま使えます。

多変量正規分布の条件つき分布③ ~観測値が得られたときの潜在変数の事後分布~

先に結果を述べると、$\boldsymbol{z_t}|\boldsymbol{y_{1:t}}$の平均・分散は以下になります。

$$
\begin{align}
\boldsymbol{\mu_t} &= E[\boldsymbol{z_t}|\boldsymbol{y_{1:t}}] = \boldsymbol{\mu_{t|t-1}} + \mathbf{K_t}\boldsymbol{r_t} \\
\mathbf{\Sigma_t} &= Cov[\boldsymbol{z_t}|\boldsymbol{y_{1:t}}] = (\mathbf{I} – \mathbf{K_t C}) \mathbf{\Sigma_{t|t-1}}
\end{align}
$$

ただし、$\boldsymbol{r_t},\mathbf{K_t}$の定義は以下です。($\mathbf{K_t}$のことをカルマンゲインといいます)

$$
\begin{align}
\boldsymbol{r_t} &\stackrel{\rm{def}}{=} \boldsymbol{y_t} – \hat{\boldsymbol{y_t}}, \\
\hat{\boldsymbol{y_t}} &\stackrel{\rm{def}}{=} E[\boldsymbol{y_t}|\boldsymbol{y_{1:t-1}}]=\mathbf{C}\boldsymbol{\mu_{t|t-1}}, \\
\mathbf{K_t} &\stackrel{\rm{def}}{=} \mathbf{\Sigma_{t|t-1}}\mathbf{C}^T\mathbf{S_t}^{-1}, \\
\mathbf{S_t} &\stackrel{\rm{def}}{=} cov[\boldsymbol{r_t}|\boldsymbol{y_{1:t-1}}] \\
&= E[\left(\mathbf{C}\boldsymbol{z_t} + \boldsymbol{\delta_t} – \hat{\boldsymbol{y_t}}\right)\left(\mathbf{C}\boldsymbol{z_t} + \boldsymbol{\delta_t} – \hat{\boldsymbol{y_t}}\right)^T] \\
&= \mathbf{C}\mathbf{\Sigma_{t|t-1}}\mathbf{C}^T + \mathbf{R}
\end{align}
$$

以下で導出します。

まず、$\mathbf{\Sigma_t}$の逆行列$\mathbf{\Sigma_t}^{-1}$は以下のようになります。(詳細は以前の記事を参照)

$$
\mathbf{\Sigma_t}^{-1} = \mathbf{\Sigma_{t|t-1}}^{-1} + \mathbf{C}^T\mathbf{R}^{-1}\mathbf{C}
$$

これの逆行列を求めるために、以下のウッドベリーの公式を用います。

$$
(\mathbf{E}-\mathbf{FH}^{-1}\mathbf{G})^{-1} = \mathbf{E}^{-1} + \mathbf{E}^{-1}\mathbf{F}(\mathbf{H}-\mathbf{GE}^{-1}\mathbf{F})^{-1}\mathbf{GE}^{-1}
$$

ウッドベリーの公式より、$\mathbf{\Sigma_t}$は以下になります。

$$
\begin{align}
\mathbf{\Sigma_t} &= \mathbf{\Sigma_{t|t-1}} – \mathbf{\Sigma_{t|t-1}}\mathbf{C}^T(\mathbf{R}+\mathbf{C\Sigma_{t|t-1}C}^T)^{-1} \mathbf{C\Sigma_{t|t-1}} \\
&= \left(\mathbf{I} – \mathbf{\Sigma_{t|t-1}}\mathbf{C}^T(\mathbf{R}+\mathbf{C\Sigma_{t|t-1}C}^T)^{-1} \mathbf{C}\right)\mathbf{\Sigma_{t|t-1}} \\
&= \left(\mathbf{I} – \mathbf{K_t C}\right) \mathbf{\Sigma_{t|t-1}}
\end{align}
$$

次に$\boldsymbol{\mu_t}$の導出です。まずこちらも以前の記事より、以下のようになります。

$$
\boldsymbol{\mu_t} = \mathbf{\Sigma_t C^T R_t^{-1}}\boldsymbol{y_t} + \mathbf{\Sigma_t \Sigma_{t|t-1}^{-1}}\boldsymbol{\mu_{t|t-1}}
$$

ここで、以下の公式を用います。(上述のウッドベリーの公式から導けます)

$$
(\mathbf{E}-\mathbf{FH}^{-1}\mathbf{G})^{-1}\mathbf{FH}^{-1} = \mathbf{E}^{-1}\mathbf{F}(\mathbf{H}-\mathbf{GE}^{-1}\mathbf{F})^{-1}
$$

上の$\boldsymbol{\mu_t}$の第1項に$\mathbf{\Sigma_t}=(\mathbf{\Sigma_{t|t-1}^{-1}} + \mathbf{C}^T\mathbf{R}^{-1}\mathbf{C})^{-1}$を代入した後、この公式を適用します。

$$
\begin{align}
\mathbf{\Sigma_t C^T R_t^{-1}}\boldsymbol{y_t} &= \left(\mathbf{\Sigma_{t|t-1}^{-1}} + \mathbf{C}^T\mathbf{R}^{-1}\mathbf{C}\right)^{-1}\mathbf{C}^T\mathbf{R}^{-1}\boldsymbol{y_t} \\
&= \mathbf{\Sigma_{t|t-1}}\mathbf{C}^T(\mathbf{R}+\mathbf{C\Sigma_{t|t-1}C^T})^{-1}\boldsymbol{y_t} \\
&= \mathbf{K_t}\boldsymbol{y_t}
\end{align}
$$

次に、$\boldsymbol{\mu_t}$の第2項にも$\mathbf{\Sigma_t}=(\mathbf{\Sigma_{t|t-1}^{-1}} + \mathbf{C}^T\mathbf{R}^{-1}\mathbf{C})^{-1}$を代入した後、ウッドベリーの公式を適用します。

$$
\begin{align}
\mathbf{\Sigma_t \Sigma_{t|t-1}^{-1}}\boldsymbol{\mu_{t|t-1}} &= (\mathbf{\Sigma_{t|t-1}^{-1}}+ \mathbf{C}^T\mathbf{R}^{-1}\mathbf{C})^{-1}\mathbf{\Sigma_{t|t-1}^{-1}}\boldsymbol{\mu_{t|t-1}} \\
&= (\mathbf{\Sigma_{t|t-1}} – \mathbf{\Sigma_{t|t-1}}\mathbf{C}^T(\mathbf{R}+\mathbf{C\Sigma_{t|t-1}C}^T)^{-1} \mathbf{C\Sigma_{t|t-1}})\mathbf{\Sigma_{t|t-1}^{-1}}\boldsymbol{\mu_{t|t-1}} \\
&= (\mathbf{\Sigma_{t|t-1}}-\mathbf{K_t}\mathbf{C}\mathbf{\Sigma_{t|t-1}})\mathbf{\Sigma_{t|t-1}^{-1}}\boldsymbol{\mu_{t|t-1}} \\
&= \boldsymbol{\mu_{t|t-1}} – \mathbf{K_t}\mathbf{C}\boldsymbol{\mu_{t|t-1}} \\
&= \boldsymbol{\mu_{t|t-1}} – \mathbf{K_t}\hat{\boldsymbol{y_t}}
\end{align}
$$

よって、$\boldsymbol{\mu_t}$は以下になります。

$$
\begin{align}
\boldsymbol{\mu_t} &= \mathbf{K_t}\boldsymbol{y_t} + \boldsymbol{\mu_{t|t-1}} – \mathbf{K_t}\hat{\boldsymbol{y_t}} \\
&= \boldsymbol{\mu_{t|t-1}} + \mathbf{K_t}\boldsymbol{r_t}
\end{align}
$$

以上で、$\boldsymbol{z_t}|\boldsymbol{y_{1:t}}$の平均$\boldsymbol{\mu_t}$と分散$\mathbf{\Sigma_t}$が求まりました。

先ほども述べたように、カルマンフィルタは$t$を1ずつ増やして逐次的に実行していく必要があるので、例えば$t$が1から100まである($\boldsymbol{y_1},\dots,\boldsymbol{y_{100}}$のデータが得られている)場合、$\boldsymbol{\mu_{100}}$だけを計算したいとしても、先に$\boldsymbol{\mu_1},\dots,\boldsymbol{\mu_{99}}$をすべて計算しないといけません。($\mathbf{\Sigma_{100}}$を計算するときも同様)

平滑化(カルマンスムーザ)

次に平滑化のアルゴリズムを紹介します。平滑化でやりたいことは、すべての観測値$\boldsymbol{y_1},\dots,\boldsymbol{y_T}$を所用とした場合の$\boldsymbol{z_t}$の分布を求めることです。

つまり、以下式の$\boldsymbol{\mu_{t|T}},\mathbf{\Sigma_{t|T}}$を求めます。

$$
p(\boldsymbol{z_t}|\boldsymbol{y_{1:T}}) = N(\boldsymbol{\mu_{t|T}}, \mathbf{\Sigma_{t|T}})
$$

この分布を求める際には、$\boldsymbol{y_{1:T}}$だけでなく、一期後の$\boldsymbol{z_{t+1}}$で条件づけた分布を考え、その後$\boldsymbol{z_{t+1}}$を積分消去します。なぜこのような手順を取るのかというと、$\boldsymbol{z_{t+1}}$を所与とすると、$\boldsymbol{z_t}$と$\boldsymbol{y_{t+1:T}}$は独立になるからです。

数式で書くと以下です。

$$
\begin{align}
p(\boldsymbol{z_t}|\boldsymbol{y_{1:T}}) &= \int p(\boldsymbol{z_t}|\boldsymbol{y_{1:T}}, \boldsymbol{z_{t+1}}) p(\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:T}})d\boldsymbol{z_{t+1}} \\
&= \int p(\boldsymbol{z_t}|\color{red}\boldsymbol{y_{1:t}} \color{black}, \boldsymbol{z_{t+1}}) p(\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:T}})d\boldsymbol{z_{t+1}}
\end{align}
$$

このように、$\boldsymbol{z_{t+1}}$で条件づけてしまえば、あとの条件は$\boldsymbol{y_{1:T}}$でも$\boldsymbol{y_{1:t}}$でも良いのです。

したがって、上の積分式内に出てくる2つの分布$p(\boldsymbol{z_t}|\boldsymbol{y_{1:t}}, \boldsymbol{z_{t+1}})$と$p(\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:T}})$を考えます。ただ、2つ目の$p(\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:T}})$を眺めると、平滑化のゴールである$p(\boldsymbol{z_t}|\boldsymbol{y_{1:T}})$と$t$が1ずれているだけです。

そこで、1期後の平滑化分布のパラメータ$\boldsymbol{\mu_{t+1|T}}$と$\mathbf{\Sigma_{t+1|T}}$は既に計算済みであるとします。そうすることで、$p(\boldsymbol{z_t}|\boldsymbol{y_{1:t}}, \boldsymbol{z_{t+1}})$だけを考えれば良いことになります。そのためには、以下の同時分布$\boldsymbol{z_t},\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:t}}$を考えます。

$$
p(\boldsymbol{z_t},\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:t}}) = N\left(\begin{pmatrix} \boldsymbol{\mu_{t|t}} \\ \boldsymbol{\mu_{t+1|t}}\end{pmatrix} , \begin{pmatrix} \mathbf{\Sigma_{t|t}} & \mathbf{\Sigma_{t|t}A}^T \\ \mathbf{A}\mathbf{\Sigma_{t|t}} & \mathbf{\Sigma_{t+1|t}}\end{pmatrix} \right)
$$

ちなみに、分散の左下成分が$\mathbf{A\Sigma_{t|t}}$になる理由は以下です。

$$
\begin{align}
Cov[\boldsymbol{z_{t+1}}, \boldsymbol{z_t}|\boldsymbol{y_{1:t}}] &= E[(\boldsymbol{z_{t+1}}-\boldsymbol{\mu_{t+1|t}})(\boldsymbol{z_t}-\boldsymbol{\mu_{t|t}})^T|\boldsymbol{y_{1:t}}] \\
&= E[\mathbf{A}(\boldsymbol{z_t}-\boldsymbol{\mu_{t|t}})(\boldsymbol{z_t}-\boldsymbol{\mu_{t|t}})^T|\boldsymbol{y_{1:t}}] \\
&= \mathbf{A \Sigma_{t|t}}
\end{align}
$$

これにより、$\boldsymbol{z_t}|\boldsymbol{y_{1:t}},\boldsymbol{z_{t+1}}$の分布は以下になります。(詳細は以前のこちらの記事を参照)

$$
\begin{align}
p(\boldsymbol{z_t}|\boldsymbol{y_{1:t}},\boldsymbol{z_{t+1}}) &= N(\boldsymbol{\mu_{t|t}}+\mathbf{\Sigma_{t|t}A}^T\mathbf{\Sigma_{t+1|t}^{-1}}(\boldsymbol{z_{t+1}}-\boldsymbol{\mu_{t+1|t}}), \mathbf{\Sigma_{t|t}} – \mathbf{\Sigma_{t|t}A}^T\mathbf{\Sigma_{t+1|t}^{-1}}\mathbf{A \Sigma_{t|t}}) \\
&= N(\boldsymbol{\mu_{t|t}}+\mathbf{J_t}(\boldsymbol{z_{t+1}}-\boldsymbol{\mu_{t+1|t}}), \mathbf{\Sigma_{t|t}} – \mathbf{J_t}\mathbf{\Sigma_{t+1|t}}\mathbf{J_t}^T)
\end{align}
$$

ただし、$\mathbf{J_t}=\mathbf{\Sigma_{t|t}A}^T\mathbf{\Sigma_{t+1|t}^{-1}}$と置いています。

ここまで来れば、後は条件つき期待値・条件つき分散の公式を用いれば、知りたい値が求められます。

まずは期待値$\boldsymbol{\mu_{t|T}}$。

$$
\begin{align}
\boldsymbol{\mu_{t|T}} &= E[\boldsymbol{z_t}|\boldsymbol{y_{1:T}}] \\
&= E\left[E[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \boldsymbol{y_{1:T}}] | \boldsymbol{y_{1:T}}\right] \\
&= E\left[E[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \color{red}\boldsymbol{y_{1:t}}\color{black}] | \boldsymbol{y_{1:T}}\right] \\
&= E\left[\boldsymbol{\mu_{t|t}}+\mathbf{J_t}(\boldsymbol{z_{t+1}}-\boldsymbol{\mu_{t+1|t}}) | \boldsymbol{y_{1:T}} \right] \\
&= \boldsymbol{\mu_{t|t}}+\mathbf{J_t}(\boldsymbol{\mu_{t+1|T}}-\boldsymbol{\mu_{t+1|t}})
\end{align}
$$

次に分散$\mathbf{\Sigma_{t|T}}$。

$$
\begin{align}
\mathbf{\Sigma_{t|T}} &= Cov[\boldsymbol{z_t}|\boldsymbol{y_{1:T}}] \\
&= Cov\left[E[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \boldsymbol{y_{1:T}}] | \boldsymbol{y_{1:T}} \right] + E\left[Cov[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \boldsymbol{y_{1:T}}] | \boldsymbol{y_{1:T}} \right] \\
&= Cov\left[E[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \color{red}\boldsymbol{y_{1:t}}\color{black}] | \boldsymbol{y_{1:T}} \right] + E\left[Cov[\boldsymbol{z_t}|\boldsymbol{z_{t+1}}, \color{red}\boldsymbol{y_{1:t}}\color{black}] | \boldsymbol{y_{1:T}} \right] \\
&= Cov\left[ \boldsymbol{\mu_{t|t}}+\mathbf{J_t}(\boldsymbol{z_{t+1}}-\boldsymbol{\mu_{t+1|t}}) | \boldsymbol{y_{1:T}} \right] + E\left[ \mathbf{\Sigma_{t|t}} – \mathbf{J_t}\mathbf{\Sigma_{t+1|t}}\mathbf{J_t}^T | \boldsymbol{y_{1:T}} \right] \\
&= \mathbf{J_t} Cov[\boldsymbol{z_{t+1}}|\boldsymbol{y_{1:T}}] \mathbf{J_t}^T + \mathbf{\Sigma_{t|t}} – \mathbf{J_t}\mathbf{\Sigma_{t+1|t}}\mathbf{J_t}^T \\
&= \mathbf{J_t\Sigma_{t+1|T}J_t}^T + \mathbf{\Sigma_{t|t}} – \mathbf{J_t}\mathbf{\Sigma_{t+1|t}}\mathbf{J_t}^T \\
&= \mathbf{\Sigma_{t|t}} + \mathbf{J_t}(\mathbf{\Sigma_{t+1|T}} – \mathbf{\Sigma_{t+1|t}})\mathbf{J_t}^T
\end{align}
$$

上記から結果だけをまとめると以下になります。

$$
\begin{align}
\boldsymbol{\mu_{t|T}} &= \boldsymbol{\mu_{t|t}}+\mathbf{J_t}(\boldsymbol{\mu_{t+1|T}}-\boldsymbol{\mu_{t+1|t}}) \\
\mathbf{\Sigma_{t|T}} &= \mathbf{\Sigma_{t|t}} + \mathbf{J_t}(\mathbf{\Sigma_{t+1|T}} – \mathbf{\Sigma_{t+1|t}})\mathbf{J_t}^T
\end{align}
$$

注意点として、先ほども述べたように$\boldsymbol{\mu_{t|T}}, \mathbf{\Sigma_{t|T}}$の計算時に1期後のパラメータ$\boldsymbol{\mu_{t+1|T}}$と$\mathbf{\Sigma_{t+1|T}}$は既に計算済みである、と仮定しました。つまり、平滑化実行の際は、カルマンフィルタと逆に$t$を1ずつ減らしながら逐次的に実行する必要があります。

また、平滑化の一番最初には$\boldsymbol{\mu_{T|T}}, \mathbf{\Sigma_{T|T}}$の値が必要です。これは、カルマンフィルタの一番最後のステップ($t$を1ずつ増やしていった最後の手順)で求められる値になります。

つまり、平滑化を行うためには必ず事前にカルマンフィルタを実行しておかなければいけない、ということになります。

実行例

以下の設定でサンプルデータを生成し、カルマンフィルタおよび平滑化を実行し結果を比較してみます。

$$
\begin{gather}
\begin{cases}
\boldsymbol{z_t} = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\boldsymbol{z_{t-1}} + \boldsymbol{\varepsilon_t},\quad \boldsymbol{\varepsilon_t} \sim N \left(\boldsymbol{0}, \begin{pmatrix}0.5 & 0 \\ 0 & 1\end{pmatrix} \right) \\
\boldsymbol{y_t} = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\boldsymbol{z_t} + \boldsymbol{\delta_t},\quad \boldsymbol{\delta_t} \sim N \left(\boldsymbol{0}, \begin{pmatrix}3 & 0 \\ 0 & 3\end{pmatrix} \right) \\
\end{cases} \\
\boldsymbol{z_1} \sim N \left(\boldsymbol{0}, \begin{pmatrix}2 & 0 \\ 0 & 2\end{pmatrix} \right)
\end{gather}
$$

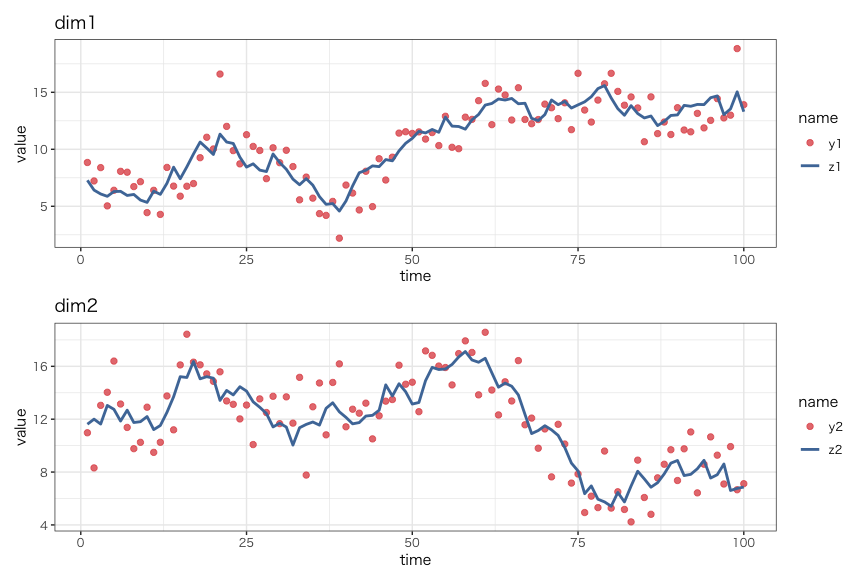
カルマンフィルタおよび平滑化を実行した結果が以下です。(赤点が観測値$y_t$、青線が状態変数$z_t$の期待値)
区間の幅として、標準偏差の2倍を設定しています。

Rでの実行コード(折りたたみ)

library(tidyverse)
library(mvnfast)
library(patchwork)
# Macでggplot日本語表示するための設定
theme_set(theme_bw(base_family = "HiraKakuProN-W3"))

# モデルのパラメータ
A <- C <- diag(2)
Q <- diag(c(0.5, 1))
R <- diag(c(3, 3))

# 時系列データの長さ
len_t <- 100

# 空の行列
z <- y <- matrix(nrow = len_t, ncol = 2)
colnames(z) <- c("z1", "z2")
colnames(y) <- c("y1", "y2")

# データ生成
set.seed(123)
for (t in c(1:len_t)) {
  if (t == 1) {
    # t=1の状態変数だけ別の分布を設定
    z[1, ] <- rmvn(1, mu = c(10, 10), sigma = diag(c(2, 2)))
  } else {
    z[t, ] <- z[t - 1, ] %*% A + rmvn(1, mu = c(0, 0), sigma = Q)
  }
  # zをもとにyを生成
  y[t, ] <- z[t, ] %*% C + rmvn(1, mu = c(0, 0), sigma = R)
}

# tibbleに格納
df <- tibble(t = c(1:len_t)) %>%
  bind_cols(z, y)

# 可視化
g1 <- df %>%
  select(t, z1, y1) %>%
  pivot_longer(-t) %>%
  ggplot(aes(x = t, y = value, color = name)) +
  geom_point(aes(shape = name), size = 3, alpha = 0.8) +
  geom_line(aes(linetype = name), linewidth = 1) +
  scale_shape_manual(values = c(20, NaN)) +
  scale_linetype_manual(values = c("blank", "solid")) +
  scale_color_manual(values = c("#E15759", "#4E79A7")) +
  labs(title = "dim1", x = "time")

g2 <- df %>%
  select(t, z2, y2) %>%
  pivot_longer(-t) %>%
  ggplot(aes(x = t, y = value, color = name)) +
  geom_point(aes(shape = name), size = 3, alpha = 0.8) +
  geom_line(aes(linetype = name), linewidth = 1) +
  scale_shape_manual(values = c(20, NaN)) +
  scale_linetype_manual(values = c("blank", "solid")) +
  scale_color_manual(values = c("#E15759", "#4E79A7")) +
  labs(title = "dim2", x = "time")

g1 / g2

# カルマンフィルタ ----------------------------------------------------------------
ssm_filtering <- function(y, A, C, Q, R, mu0, Q0) {
  len_y <- nrow(y)
  dim_y <- ncol(y)

  # 一期先の予測分布のパラメータ
  mu_pred <- matrix(0, nrow = len_y, ncol = dim_y)
  Sigma_pred <- array(dim = c(len_y, dim_y, dim_y))

  # 同時点の分布のパラメータ
  mu_filter <- matrix(0, nrow = len_y, ncol = dim_y)
  Sigma_filter <- array(dim = c(len_y, dim_y, dim_y))

  for (t in c(1:len_y)) {
    # prediction step
    if (t == 1) {
      mu_pred[1, ] <- mu0
      Sigma_pred[1, , ] <- Q0
    } else {
      mu_pred[t, ] <- mu_filter[t - 1, ] %*% A
      Sigma_pred[t, , ] <- A %*% Sigma_filter[t - 1, , ] %*% t(A) + Q
    }

    # measurement step
    S_t <- C %*% Sigma_pred[t, , ] %*% C + R
    K_t <- Sigma_pred[t, , ] %*% t(C) %*% solve(S_t)
    r_t <- y[t, ] - mu_pred[t, ] %*% C
    mu_filter[t, ] <- mu_pred[t, ] + r_t %*% K_t
    Sigma_filter[t, , ] <- (diag(dim_y) - K_t %*% C) %*% Sigma_pred[t, , ]
  }

  return(list("mu_filter" = mu_filter, "Sigma_filter" = Sigma_filter, "mu_pred" = mu_pred, "Sigma_pred" = Sigma_pred))
}

# カルマンフィルタ実行
param_filtering <- ssm_filtering(y, A, C, Q, R, c(10, 10), diag(c(100, 100)))

# 結果をtibbleに格納
df_filter <- select(df, t, y1, y2) %>%
  mutate(
    mu1 = param_filtering$mu_filter[, 1],
    # 上限・下限として標準偏差の2倍を設定
    upr1 = mu1 + 2 * sqrt(param_filtering$Sigma_filter[, 1, 1]),
    lwr1 = mu1 - 2 * sqrt(param_filtering$Sigma_filter[, 1, 1]),
    mu2 = param_filtering$mu_filter[, 2],
    # 上限・下限として標準偏差の2倍を設定
    upr2 = mu2 + 2 * sqrt(param_filtering$Sigma_filter[, 2, 2]),
    lwr2 = mu2 - 2 * sqrt(param_filtering$Sigma_filter[, 2, 2])
  )

g1_filter <- ggplot(df_filter, aes(x = t)) +
  geom_point(aes(y = y1), size = 3, alpha = 0.8, color = "#E15759") +
  geom_line(aes(y = mu1), linewidth = 1, color = "#4E79A7") +
  geom_ribbon(aes(ymax = upr1, ymin = lwr1), fill = "#4E79A7", alpha = 0.3) +
  labs(title = "dim1 (カルマンフィルタ)", x = "time")

g2_filter <- ggplot(df_filter, aes(x = t)) +
  geom_point(aes(y = y2), size = 3, alpha = 0.8, color = "#E15759") +
  geom_line(aes(y = mu2), linewidth = 1, color = "#4E79A7") +
  geom_ribbon(aes(ymax = upr2, ymin = lwr2), fill = "#4E79A7", alpha = 0.3) +
  labs(title = "dim2 (カルマンフィルタ)", x = "time")

g1_filter / g2_filter

# 平滑化 ---------------------------------------------------------------------
ssm_smoothing <- function(C, mu_filter, Sigma_filter, mu_pred, Sigma_pred) {
  len_y <- nrow(y)
  dim_y <- ncol(y)
  mu_smooth <- matrix(0, nrow = len_y, ncol = dim_y)
  Sigma_smooth <- array(dim = c(len_y, dim_y, dim_y))

  for (t in c(len_y:1)) {
    if (t == len_y) {
      mu_smooth[len_y, ] <- mu_filter[len_y, ]
      Sigma_smooth[len_y, , ] <- Sigma_filter[len_y, , ]
    } else {
      J_t <- Sigma_filter[t, , ] %*% t(A) %*% solve(Sigma_pred[t + 1, , ])
      mu_smooth[t, ] <- mu_filter[t, ] + (mu_smooth[t + 1, ] - mu_pred[t + 1, ]) %*% J_t
      Sigma_smooth[t, , ] <- Sigma_filter[t, , ] + J_t %*% (Sigma_smooth[t + 1, , ] - Sigma_pred[t + 1, , ]) %*% t(J_t)
    }
  }
  return(list("mu_smooth" = mu_smooth, "Sigma_smooth" = Sigma_smooth))
}

# 平滑化実行
param_smoothing <- ssm_smoothing(
  C,
  param_filtering$mu_filter,
  param_filtering$Sigma_filter,
  param_filtering$mu_pred,
  param_filtering$Sigma_pred
)

df_smooth <- select(df, t, y1, y2) %>%
  mutate(
    mu1 = param_smoothing$mu_smooth[, 1],
    # 上限・下限として標準偏差の2倍を設定
    upr1 = mu1 + 2 * sqrt(param_smoothing$Sigma_smooth[, 1, 1]),
    lwr1 = mu1 - 2 * sqrt(param_smoothing$Sigma_smooth[, 1, 1]),
    mu2 = param_smoothing$mu_smooth[, 2],
    # 上限・下限として標準偏差の2倍を設定
    upr2 = mu2 + 2 * sqrt(param_smoothing$Sigma_smooth[, 2, 2]),
    lwr2 = mu2 - 2 * sqrt(param_smoothing$Sigma_smooth[, 2, 2])
  )

g1_smooth <- ggplot(df_smooth, aes(x = t)) +
  geom_point(aes(y = y1), size = 3, alpha = 0.8, color = "#E15759") +
  geom_line(aes(y = mu1), linewidth = 1, color = "#4E79A7") +
  geom_ribbon(aes(ymax = upr1, ymin = lwr1), fill = "#4E79A7", alpha = 0.3) +
  labs(title = "dim1 (平滑化)", x = "time")

g2_smooth <- ggplot(df_smooth, aes(x = t)) +
  geom_point(aes(y = y2), size = 3, alpha = 0.8, color = "#E15759") +
  geom_line(aes(y = mu2), linewidth = 1, color = "#4E79A7") +
  geom_ribbon(aes(ymax = upr2, ymin = lwr2), fill = "#4E79A7", alpha = 0.3) +
  labs(title = "dim2 (平滑化)", x = "time")

# カルマンフィルタと平滑化を比較
(g1_filter | g1_smooth) / (g2_filter | g2_smooth)

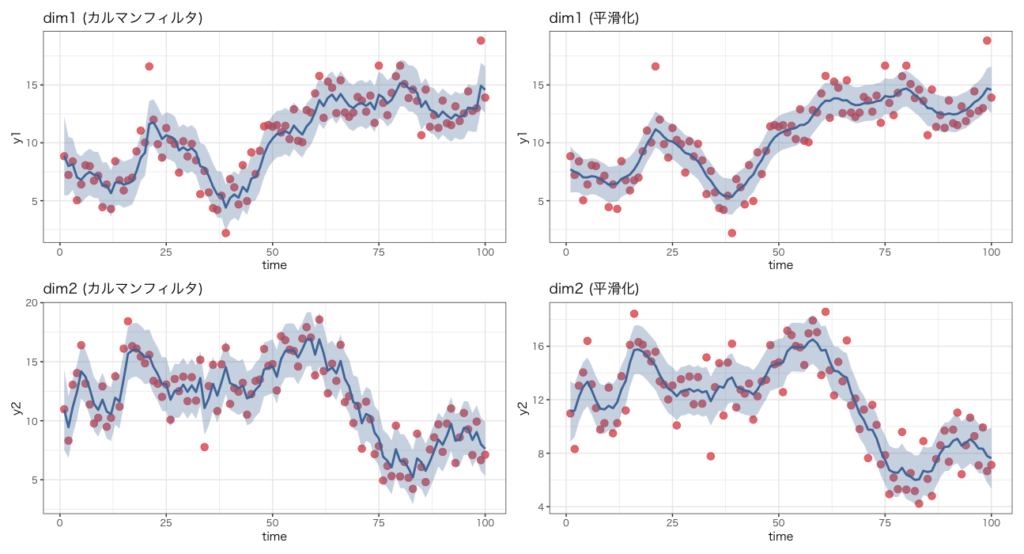
カルマンフィルタと平滑化の結果を比較すると、カルマンフィルタのほうが変動が大きく、平滑化は滑らかに動いています。これは、カルマンフィルタでは$z_t$の分布の推定に同時点までの観測値($y_1,\dots,y_t$)しか使っていない一方、平滑化ではすべての観測値($y_1,\dots,y_T$)を使って$z_t$の分布を推定していることが理由です。つまり、平滑化ではカルマンフィルタよりもより多くの情報を使っているので不確実性が減少するのです。

しかし、平滑化実行の際には必ず事前にカルマンフィルタも実行しないといけないので、計算量の面ではカルマンフィルタのほうに軍配が上がります。また、最新の状態変数$z_T$の分布はカルマンフィルタも平滑化も同じ結果となるので、$z_T$の分布だけ知りたい場合、平滑化を実行するメリットは0となります。

まとめ

今回は、線形ガウス状態空間モデルの推論アルゴリズムであるカルマンフィルタと平滑化をご紹介しました。

ただ、今回は既知としましたが、実際は状態変数だけでなくその他のパラメータ($A$や$R$、$Q$など)もデータから推定する必要があります。

これらのパラメータの推定方法については次回ご紹介しようと思います。

参考：Kevin P. Murphy『Machine Learning: a Probabilistic Perspective』