前回のまとめ
前回は、変数$\boldsymbol{x}=(\boldsymbol{x_1}, \boldsymbol{x_2})$が多変量正規分布$MVN(\boldsymbol{\mu},\mathbf{\Sigma})$にしたがい、かつ$\boldsymbol{x_2}$が既知のときの、$\boldsymbol{x_1}|\boldsymbol{x_2}$の平均・分散が以下で表せることを示しました。
$$
\begin{align*}
p(\boldsymbol{x_1}|\boldsymbol{x_2}) &= N(\boldsymbol{x_1}|\boldsymbol{\mu_{1|2}},\mathbf{\Sigma_{1|2}}) \\
\boldsymbol{\mu_{1|2}} & = \boldsymbol{\mu_1} + \mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2}) \\
\mathbf{\Sigma_{1|2}} &= \mathbf{\Sigma_{11}} – \mathbf{\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}} \\
&= \mathbf{\Lambda_{11}^{-1}}
\end{align*}
$$
ただし、各パラメータの定義は以下です。
$$
\boldsymbol{\mu}=\begin{pmatrix}\boldsymbol{\mu_1} \\
\boldsymbol{\mu_2}\end{pmatrix}, \
\mathbf{\Sigma}=\begin{pmatrix}\mathbf{\Sigma_{11}} & \mathbf{\Sigma_{12}} \\
\mathbf{\Sigma_{21}} & \mathbf{\Sigma_{22}} \end{pmatrix}, \
\mathbf{\Lambda} = \mathbf{\Sigma}^{-1}=\begin{pmatrix}\mathbf{\Lambda_{11}} & \mathbf{\Lambda_{12}} \\
\mathbf{\Lambda_{21}} & \mathbf{\Lambda_{22}} \end{pmatrix}
$$
今回はこの定理を使い、線形ガウスシステムの紹介をしていきます。
線形ガウスシステム
今回紹介するモデルには、2種の確率変数$\boldsymbol{x}$と$\boldsymbol{y}$が登場します。一つ目の$\boldsymbol{x}$は潜在変数で、実際の値を観測することはできません。一方の$\boldsymbol{y}$はその値を観測できるものとします。
また、この$\boldsymbol{x}$と$\boldsymbol{y}$の間には、以下の関係があるとします。
$$
\begin{align}
p(\boldsymbol{x}) &= N(\boldsymbol{x} | \boldsymbol{\mu_x}, \mathbf{\Sigma_x}) \\
p(\boldsymbol{y}|\boldsymbol{x}) &= N(\boldsymbol{y} | \mathbf{A}\boldsymbol{x} + \boldsymbol{b}, \mathbf{\Sigma_y})
\end{align}
$$
この式が意味しているのは、まず人間が観測不可能な変数$\boldsymbol{x}$が生成され、この$\boldsymbol{x}$をもとに人間が観測できる変数$\boldsymbol{y}$が生成される、というメカニズムです。
今回は、観測値$\boldsymbol{y}$から得られる情報を使い、この神のみぞ知る$\boldsymbol{x}$を推測するための事後分布$p(\boldsymbol{x}|\boldsymbol{y})$を求める方法をご紹介します。
事後分布の導出
$\boldsymbol{x}$と$\boldsymbol{y}$の同時分布$p(\boldsymbol{x}, \boldsymbol{y})$は、以下のように変形できます。
$$
p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{x}) p(\boldsymbol{y}|\boldsymbol{x})
$$
上式を対数化し、より詳細な式を書き下してみます。(ただし、定数項は除外)
$$
\log p(\boldsymbol{x}, \boldsymbol{y}) = -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu_x})^T\mathbf{\Sigma_x}^{-1}(\boldsymbol{x}-\boldsymbol{\mu_x}) -\frac{1}{2}(\boldsymbol{y} – \mathbf{A}\boldsymbol{x} – \boldsymbol{b})^T\mathbf{\Sigma_y}^{-1}(\boldsymbol{y} – \mathbf{A}\boldsymbol{x} – \boldsymbol{b})
$$
これを展開し、$\boldsymbol{x}, \boldsymbol{y}$の2次の項だけ残して整理すると以下になります。
(定数項や1次の項は無視します)
$$
\begin{align}
Q &= -\frac{1}{2}\boldsymbol{x}^T\mathbf{\Sigma_x^{-1}}\boldsymbol{x}-\frac{1}{2}\boldsymbol{y}^T\mathbf{\Sigma_y^{-1}}\boldsymbol{y}-\frac{1}{2}(\mathbf{A}\boldsymbol{x})^T\mathbf{\Sigma_y^{-1}}(\mathbf{A}\boldsymbol{x})+\boldsymbol{y}^T\mathbf{\Sigma_y^{-1}}\mathbf{A}\boldsymbol{x} \\
&= -\frac{1}{2}\begin{pmatrix}\boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix}^T\begin{pmatrix} \mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A} & -\mathbf{A}^T\mathbf{\Sigma_y^{-1}} \\ -\mathbf{\Sigma_y^{-1}}\mathbf{A} & \mathbf{\Sigma_y^{-1}} \end{pmatrix} \begin{pmatrix} \boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix} \\
&= -\frac{1}{2}\begin{pmatrix}\boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix}^T \mathbf{\Sigma}^{-1}\begin{pmatrix} \boldsymbol{x} \\ \boldsymbol{y} \end{pmatrix}
\end{align}
$$
ただし、最終行の$\mathbf{\Sigma}^{-1}$の定義は以下です。
$$
\begin{align}
\mathbf{\Sigma}^{-1} &= \begin{pmatrix} \mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A} & -\mathbf{A}^T\mathbf{\Sigma_y^{-1}} \\ -\mathbf{\Sigma_y^{-1}}\mathbf{A} & \mathbf{\Sigma_y^{-1}} \end{pmatrix} \\
&= \begin{pmatrix} \mathbf{\Sigma_{xx}} & \mathbf{\Sigma_{xy}} \\ \mathbf{\Sigma_{yx}} & \mathbf{\Sigma_{yy}} \end{pmatrix}^{-1} \\
& \stackrel{\mathrm{def}}{=} \begin{pmatrix}\mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{pmatrix} =\mathbf{\Lambda}
\end{align}
$$
これで同時分布の精度行列(=共分散行列の逆行列)である$\mathbf{\Sigma}^{-1}=\mathbf{\Lambda}$が求められました。この結果と、前回紹介した条件つき分布の定理を使うと、$\boldsymbol{x}|\boldsymbol{y}$の分散$\mathbf{\Sigma_{x|y}}$は以下になることが分かります。
$$
\mathbf{\Sigma_{x|y}} = \mathbf{\Lambda_{xx}}^{-1} = (\mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A})^{-1}
$$
次に、平均$\boldsymbol{\mu_{x|y}}$を求めます。下準備として、$\mathbf{\Sigma}^{-1}=\mathbf{\Lambda}$から、
$$
\mathbf{\Lambda_{xy}} = -\mathbf{\Lambda_{xx}}\mathbf{\Sigma_{xy}\Sigma_{yy}^{-1}}
$$
が成り立つことが分かります。これを少し変形して、以下の形にしておきます。
$$
\mathbf{\Sigma_{xy}\Sigma_{yy}^{-1}} = -\mathbf{\Lambda_{xx}^{-1}\Lambda_{xy}}
$$
詳細については、2つ前のこちらの投稿を参照してください。
条件つき分布の定理から、$\boldsymbol{x}|\boldsymbol{y}$の平均は$\boldsymbol{\mu_{x|y}}=\boldsymbol{\mu_x}+\mathbf{\Sigma_{xy}\Sigma_{yy}^{-1}}(\boldsymbol{y}-\boldsymbol{\mu_y})$となるのですが、式中の$\mathbf{\Sigma_{xy}\Sigma_{yy}^{-1}}$の部分は、先ほどの下準備の式で置き換えることができるので、結果以下のようになります。
$$
\begin{align}
\boldsymbol{\mu_{x|y}} &= \boldsymbol{\mu_x} – \mathbf{\Lambda_{xx}^{-1}\Lambda_{xy}}(\boldsymbol{y}-\boldsymbol{\mu_y}) \\
&= \mathbf{\Lambda_{xx}}^{-1} \left( \mathbf{\Lambda_{xx}}\boldsymbol{\mu_x} – \mathbf{\Lambda_{xy}} (\boldsymbol{y}-\boldsymbol{\mu_y}) \right) \\
&= \mathbf{\Sigma_{x|y}} \left[ (\mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A})\boldsymbol{\mu_x} + \mathbf{A}^T\mathbf{\Sigma_y^{-1}} (\boldsymbol{y}-\boldsymbol{\mu_y}) \right]
\end{align}
$$
$p(\boldsymbol{y}|\boldsymbol{x}) = N(\boldsymbol{y} | \mathbf{A}\boldsymbol{x} + \boldsymbol{b}, \mathbf{\Sigma_y})$から、明らかに$\boldsymbol{\mu_{y}}=\mathbf{A}\boldsymbol{\mu_x}+\boldsymbol{b}$ですので、$\boldsymbol{\mu_y}$を置き換えます。
$$
\begin{align}
\boldsymbol{\mu_{x|y}} &= \mathbf{\Sigma_{x|y}} \left[ (\mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A})\boldsymbol{\mu_x} + \mathbf{A}^T\mathbf{\Sigma_y^{-1}} (\boldsymbol{y}-\boldsymbol{\mu_y}) \right] \\
&= \mathbf{\Sigma_{x|y}} \left[ (\mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A})\boldsymbol{\mu_x} + \mathbf{A}^T\mathbf{\Sigma_y^{-1}} (\boldsymbol{y}-\mathbf{A}\boldsymbol{\mu_x}-\boldsymbol{b}) \right] \\
&= \mathbf{\Sigma_{x|y}} \left[ \mathbf{\Sigma_x^{-1}}\boldsymbol{\mu_x} + \mathbf{A}^T\mathbf{\Sigma_y^{-1}} (\boldsymbol{y}-\boldsymbol{b}) \right]
\end{align}
$$
以上をまとめると、$\boldsymbol{x}|\boldsymbol{y}$の分布は以下のようになります。
$$
\begin{align*}
p(\boldsymbol{x}|\boldsymbol{y}) &= N(\boldsymbol{x}|\boldsymbol{\mu_{x|y}},\mathbf{\Sigma_{x|y}}) \\
\mathbf{\Sigma_{x|y}} &= \mathbf{\Lambda_{xx}}^{-1} = (\mathbf{\Sigma_x^{-1}}+\mathbf{A}^T\mathbf{\Sigma_y^{-1}A})^{-1} \\
\boldsymbol{\mu_{x|y}} & = \mathbf{\Sigma_{x|y}} \left[ \mathbf{\Sigma_x^{-1}}\boldsymbol{\mu_x} + \mathbf{A}^T\mathbf{\Sigma_y^{-1}} (\boldsymbol{y}-\boldsymbol{b}) \right]
\end{align*}
$$
Rでの実装例
簡単な例をRで実装してみます。$x$をもとにして、以下の分布から$n$個の観測値$y_i$が生成されるとします。
$$
y_i \sim N(x+b, \sigma_y^2)
$$
$\mathbf{A}$を1を$n$個並べたベクトル($\mathbf{A}=(1,\dots,1)^T$)、$\boldsymbol{b}$を$b$を$n$個並べたベクトル($\boldsymbol{b}=(b,\dots,b)^T$)とすると、$\boldsymbol{y}=(y_1,\dots,y_n)$は多変量正規分布にしたがう変数として定義できます。
$$
\boldsymbol{y} \sim MVN(\mathbf{A}x + \boldsymbol{b}, \sigma_y^2\mathbf{I})
$$
実際に、以下の設定で$\boldsymbol{y}$を生成してみます。
- $x=3$
- $n=10$
- $b=-2$
- $\sigma_y=2$
library(tidyverse)
x = 3
n = 10
A = rep(1, n)
b = -2
sig_y = 2
# yの精度(分散の逆数)
lambda_y = 1 / (sig_y)^2
# yを生成
set.seed(123)
eps = rnorm(n, 0, sig_y)
y = A * x + b + eps
summary(y)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
#-1.53012 -0.06354 0.84033 1.14925 1.75602 4.43013 この$\boldsymbol{y}$をもとに、$x$の事後分布を求めていきます。$x$の事前分布$x\sim N(\mu_x, \sigma_x^2)$に対して、$\mu_x=0, \sigma_x=5$に設定します。
mu_x_prior = 0
sig_x_prior = 5
lambda_x_prior = 1 / (sig_x_prior^2)そして、事後分布の精度$\lambda_{x|y}$と標準偏差$\sigma_{x|y}$、平均$\mu_{x|y}$を求めます。
$$
\begin{align}
\lambda_{x|y} &= \lambda_x + \mathbf{A}^T\mathbf{A}\lambda_y \\
&= \lambda_x + n\lambda_y \\
\sigma_{x|y} &= \frac{1}{\sqrt{\lambda_{x|y}}} \\
\mu_{x|y} &= \frac{1}{\lambda_{x|y}}(\lambda_x\mu_x + \lambda_y\mathbf{A}^T(\boldsymbol{y-b}))
\end{align}
$$
lambda_x_porsterior = lambda_x_prior + as.numeric(A%*%A)*lambda_y
sig_x_posterior = 1 / sqrt(lambda_x_porsterior)
mu_x_posterior = (lambda_x_prior*mu_x_prior + as.numeric(A%*%(y-b))*lambda_y) / lambda_x_porsterior事後分布の平均と標準偏差が求められたので、事前分布と合わせて可視化してみます。
x_seq = seq(-10, 10, length=1000)
# 事前分布の密度
dens_prior = dnorm(x_seq, mu_x_prior, sig_x_prior)
# 事後分布の密度
dens_posterior = dnorm(x_seq, mu_x_posterior, sig_x_posterior)
# データフレームにまとめる
df_dens = tibble(x=x_seq, prior=dens_prior, posterior=dens_posterior) %>%
pivot_longer(-x, names_to="density", values_to="value")
# 可視化
ggplot(df_dens, aes(x=x, y=value, color=density)) +
geom_line(alpha=0.7) +
geom_vline(xintercept=3, linetype="dashed", alpha=0.5) +
labs(y="density")結果が以下です。事前分布(青の曲線)は比較的フラットですが、事後分布(赤の曲線)は真の値$x=3$(グラフの垂直線)のまわりに集中しています。これは、事前分布がデータによって更新されていることを表しています。
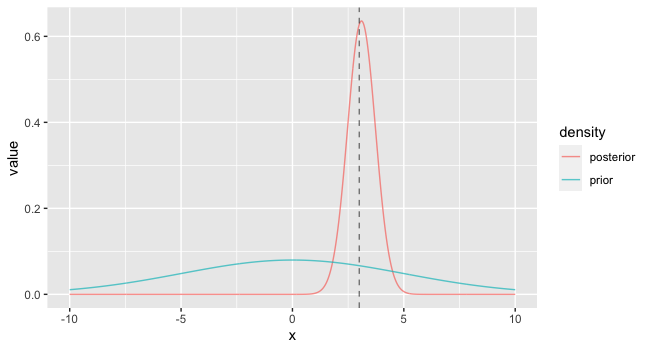
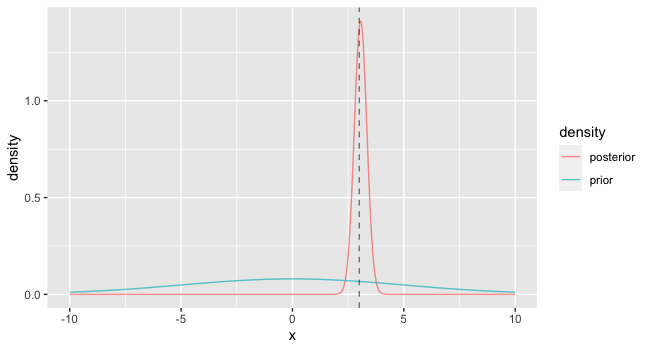
ちなみに、$n$を10から50まで増やすと以下のようにさらに$x=3$のまわりに集中します。
使用ケース
線形ガウスシステムが使われるケースとして、例えば主成分分析や因子分析の確率モデル版があります。
つまり、データ$\boldsymbol{y}$が得られたときに、その背後に主成分や因子$\boldsymbol{x}$の存在を仮定し、この線形ガウスシステムを用いることで、$\boldsymbol{x}$の事後分布や事後期待値を求めることができます。
主成分分析の確率モデル版(PPCA)については、以前ブログに書きましたのでよろしければそちらもご覧ください。
まとめ
今回は、線形ガウスシステムを使って$y$が所与のときの$x$の分布を導出してみました。
『多変量正規分布の条件つき分布』について3回に渡って書いてきましたが、このシリーズは今回で一旦終わろうと思います。
このシリーズの延長として、上で触れた確率モデル版因子分析について今後投稿するかもしれません。(時期未定)
参考: