ベイズ統計で頻出する多変量正規分布の条件つき分布の導出について、複数回に分けて投稿していきます。
前回は、導出の際に使用するブロック行列の逆行列・行列式についてまとめました。
今回は、多変量正規分布の密度関数を変形し、条件つき分布の密度関数を導出し、分布の平均・分散を求めます。
前回のまとめ & 今回のゴール
以下の正方行列$\mathbf{M}$を考えます。
$$
\mathbf{M} = \begin{pmatrix} \mathbf{E} & \mathbf{F} \\ \mathbf{G} & \mathbf{H} \end{pmatrix}
$$
このとき、$\mathbf{M}$の$\mathbf{H}$に関するシューア補行列$\mathbf{M/H} = \mathbf{E} – \mathbf{FH}^{-1}\mathbf{G}$を使って、$\mathbf{M}$を以下のように変形できることを示しました。
$$
\begin{align}
\mathbf{M} &= \begin{pmatrix} \mathbf{I} & \mathbf{FH}^{-1} \\ \mathbf{O} & \mathbf{I} \end{pmatrix}
\begin{pmatrix}\mathbf{M}/\mathbf{H} & \mathbf{O} \\ \mathbf{O} & \mathbf{H} \end{pmatrix}
\begin{pmatrix}\mathbf{I} & \mathbf{O} \\ \mathbf{H}^{-1}\mathbf{G} & \mathbf{I} \end{pmatrix} \\
\mathbf{M}^{-1} &= \begin{pmatrix}\mathbf{I} & \mathbf{O} \\ -\mathbf{H}^{-1}\mathbf{G} & \mathbf{I} \end{pmatrix}
\begin{pmatrix}(\mathbf{M}/\mathbf{H})^{-1} & \mathbf{O} \\ \mathbf{O} & \mathbf{H}^{-1}\end{pmatrix}
\begin{pmatrix}\mathbf{I} & -\mathbf{FH}^{-1} \\ \mathbf{O} & \mathbf{I} \end{pmatrix}
\end{align}
$$
また、行列式$|\mathbf{M}|$は以下のように求められることも示しました。
$$
|\mathbf{M}| = |\mathbf{M}/\mathbf{H}| |\mathbf{H}|
$$
今回はこれらを使い、$\boldsymbol{x}=(\boldsymbol{x_1}, \boldsymbol{x_2})$が多変量正規分布$MVN(\boldsymbol{\mu},\mathbf{\Sigma})$にしたがい、かつ$\boldsymbol{x_2}$が既知のときの平均・分散が以下で表せることを示していきます。
$$
\begin{align*}
p(\boldsymbol{x_1}|\boldsymbol{x_2}) &= N(\boldsymbol{x_1}|\boldsymbol{\mu_{1|2}},\mathbf{\Sigma_{1|2}}) \\
\boldsymbol{\mu_{1|2}} & = \boldsymbol{\mu_1} + \mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2}) \\
\mathbf{\Sigma_{1|2}} &= \mathbf{\Sigma_{11}} – \mathbf{\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}} \\
&= \mathbf{\Lambda_{11}^{-1}}
\end{align*}
$$
ただし、各パラメータの定義は以下です。
$$
\boldsymbol{\mu}=\begin{pmatrix}\boldsymbol{\mu_1} \\
\boldsymbol{\mu_2}\end{pmatrix}, \
\mathbf{\Sigma}=\begin{pmatrix}\mathbf{\Sigma_{11}} & \mathbf{\Sigma_{12}} \\
\mathbf{\Sigma_{21}} & \mathbf{\Sigma_{22}} \end{pmatrix}, \
\mathbf{\Lambda} = \mathbf{\Sigma}^{-1}=\begin{pmatrix}\mathbf{\Lambda_{11}} & \mathbf{\Lambda_{12}} \\
\mathbf{\Lambda_{21}} & \mathbf{\Lambda_{22}} \end{pmatrix}
$$
証明
$D$次元の確率変数$\boldsymbol{x}$の密度関数は以下になります。
$$
\frac{1}{(2\pi)^{D/2}|\mathbf{\Sigma}|^{1/2}}\exp \left[ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \mathbf{\Sigma^{-1}} (\boldsymbol{x}-\boldsymbol{\mu})\right]
$$
この式の指数部分だけを取り出してみます。
$$
\begin{align}
E &= \exp \left[ -\frac{1}{2} (\boldsymbol{x}-\boldsymbol{\mu})^T \mathbf{\Sigma^{-1}} (\boldsymbol{x}-\boldsymbol{\mu}) \right] \\
&= \exp \left[
-\frac{1}{2} \begin{pmatrix} \boldsymbol{x_1}-\boldsymbol{\mu_1} \\ \boldsymbol{x_2}-\boldsymbol{\mu_2} \end{pmatrix}^T
\begin{pmatrix} \mathbf{\Sigma_{11}} & \mathbf{\Sigma_{12}} \\ \mathbf{\Sigma_{21}} & \mathbf{\Sigma_{22}} \end{pmatrix}^{-1}
\begin{pmatrix} \boldsymbol{x_1}-\boldsymbol{\mu_1} \\ \boldsymbol{x_2}-\boldsymbol{\mu_2}\end{pmatrix}
\right]
\end{align}
$$
ここで、上述の$\mathbf{M}^{-1} = \begin{pmatrix}\mathbf{I} & \mathbf{O} \\ -\mathbf{H}^{-1}\mathbf{G} & \mathbf{I} \end{pmatrix}
\begin{pmatrix}(\mathbf{M}/\mathbf{H})^{-1} & \mathbf{O} \\ \mathbf{O} & \mathbf{H}^{-1}\end{pmatrix}
\begin{pmatrix}\mathbf{I} & -\mathbf{FH}^{-1} \\ \mathbf{O} & \mathbf{I} \end{pmatrix}$を用い、$E$の中の$\mathbf{\Sigma}^{-1}$を変形します。
$$
\begin{align}
E &= \exp \Big[
-\frac{1}{2} \begin{pmatrix} \boldsymbol{x_1}-\boldsymbol{\mu_1} \\ \boldsymbol{x_2}-\boldsymbol{\mu_2} \end{pmatrix}^T
\begin{pmatrix} \mathbf{I} & \mathbf{O} \\ -\mathbf{\Sigma_{22}^{-1}}\mathbf{\Sigma_{21}} & \mathbf{I} \end{pmatrix}
\begin{pmatrix}(\mathbf{\Sigma}/\mathbf{\Sigma_{22}})^{-1} & \mathbf{O} \\ \mathbf{O} & \mathbf{\Sigma_{22}^{-1}}\end{pmatrix} \\
& \qquad\qquad \times \begin{pmatrix} \mathbf{I} & -\mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}} \\ \mathbf{O} & \mathbf{I} \end{pmatrix}\begin{pmatrix} \boldsymbol{x_1}-\boldsymbol{\mu_1} \\ \boldsymbol{x_2}-\boldsymbol{\mu_2}\end{pmatrix}
\Big] \\
&= \exp \bigg[
-\frac{1}{2} (\boldsymbol{x_1}-\boldsymbol{\mu_1}-\mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2}))^T(\mathbf{\Sigma}/\mathbf{\Sigma_{22}})^{-1} \\
& \qquad \qquad (\boldsymbol{x_1}-\boldsymbol{\mu_1}-\mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2})) \bigg] \\
& \quad \times \exp \left[ -\frac{1}{2}(\boldsymbol{x_2}-\boldsymbol{\mu_2})^T\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2})\right]
\end{align}
$$
上の式は、
$$
\exp(\boldsymbol{x_1},\boldsymbol{x_2}\text{の2次形式}) \times \exp(\boldsymbol{x_2}\text{の2次形式})
$$
となっています。よって$p(\boldsymbol{x})=p(\boldsymbol{x_1},\boldsymbol{x_2})$は次のように分解することができます。
$$
\begin{align}
p(\boldsymbol{x_1},\boldsymbol{x_2}) &= p(\boldsymbol{x_1}|\boldsymbol{x_2}) p(\boldsymbol{x_2}) \\
&= N(\boldsymbol{x_1}|\boldsymbol{\mu_{1|2}},\mathbf{\Sigma_{1|2}})N(\boldsymbol{x_2}|\boldsymbol{\mu_2},\mathbf{\Sigma_2})
\end{align}
$$
$\boldsymbol{\mu_{1|2}}$、$\mathbf{\Sigma_{1|2}}$は、上の$E$の式から以下のようになることが分かります。
$$
\begin{align}
\boldsymbol{\mu_{1|2}} &= \boldsymbol{\mu_1} + \mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2}) \\
\mathbf{\Sigma_{1|2}} &= \mathbf{\Sigma}/\mathbf{\Sigma_{22}} = \mathbf{\Sigma_{11}} – \mathbf{\Sigma_{12}\Sigma_{22}}^{-1}\mathbf{\Sigma_{21}}
\end{align}
$$
これだけでも$\boldsymbol{x_1}|\boldsymbol{x_2}$の分布は分かりますが、念のため正則化項も正しい形になっているかチェックします。
$d_1=\dim(\boldsymbol{x_1}),d_2=\dim(\boldsymbol{x_2})$とすると、$|\mathbf{M}| = |\mathbf{M}/\mathbf{H}| |\mathbf{H}|$を使って、正則化項は次のように変形できます。
$$
\begin{align}
(2\pi)^{(d_1+d_2)/2}|\mathbf{\Sigma}|^{1/2} &= (2\pi)^{(d_1+d_2)/2}(|\mathbf{\Sigma}/\mathbf{\Sigma_{22}}| |\mathbf{\Sigma_{22}}|)^{1/2} \\
&= (2\pi)^{d_1/2}|\mathbf{\Sigma}/\mathbf{\Sigma_{22}}| (2\pi)^{d_2/2} |\mathbf{\Sigma_{22}}|^{1/2} \\
&= (2\pi)^{d_1/2}|\mathbf{\Sigma_{1|2}}|^{1/2} (2\pi)^{d_2/2} |\mathbf{\Sigma_{22}}|^{1/2}
\end{align}
$$
この式の前半が$N(\boldsymbol{x_1}|\boldsymbol{\mu_{1|2}},\mathbf{\Sigma_{1|2}})$の、後半が$N(\boldsymbol{x_2}|\boldsymbol{\mu_2},\mathbf{\Sigma_{22}})$の正則化項となっていることが分かります。
(証明終)
例:2次元正規分布の条件つき分布
以上を簡単な2次元正規分布で確認してみましょう。設定は以下のようにします。
$$
\boldsymbol{\mu} = \begin{pmatrix}0 \\ 1 \end{pmatrix}, \mathbf{\Sigma}=\begin{pmatrix}1 & 1 \\ 1 & 4 \end{pmatrix}
$$
密度関数は以下のようになります。
$$
f(\boldsymbol{x}) = \frac{1}{2\pi |\mathbf{\Sigma}|^{1/2}} \exp \left[ -\frac{1}{2} \begin{pmatrix} x_1 \\ x_2 – 1 \end{pmatrix}^T \begin{pmatrix}1 & 1 \\ 1 & 4\end{pmatrix}^{-1}\begin{pmatrix}x_1 \\ x_2-1\end{pmatrix}\right]
$$
Rでこの関数を定義してみます。
library(tidyverse)
library(patchwork)
# 2次元正規分布の密度関数を定義
mvn_pdf = function(
x1,
x2,
mu=c(0, 0),
cov=matrix(c(1, 0, 0, 1), nrow=2)
){
x = c(x1, x2)
# 指数部分を計算
E = exp(-0.5 * (t(x-mu) %*% solve(cov) %*% (x-mu))) %>%
as.numeric()
# 正規化項を計算
nrm = 2*pi * det(cov)^0.5
return(E / nrm)
}
# 平均・分散
mu = c(0, 1)
cov = c(1, 1, 1, 4) %>%
matrix(nrow=2, byrow=T)この分布の密度関数を、等高線を使って描画してみます。
# x1, x2の図示範囲を設定
x1 = seq(-3, 3, length=100)
x2 = seq(-4, 6, length=100)
# x1, x2の値の全組み合わせを作り、各組み合わせのときの密度を計算
df_x = expand_grid(x1, x2) %>%
mutate(dens=map2_dbl(x1, x2, ~mvn_pdf(x1=.x, x2=.y, mu=mu, cov=cov)))
# 等高線で図示
g_mvn = ggplot(df_x, aes(x=x1, y=x2, z=dens, color=..level..)) +
geom_contour()
g_mvn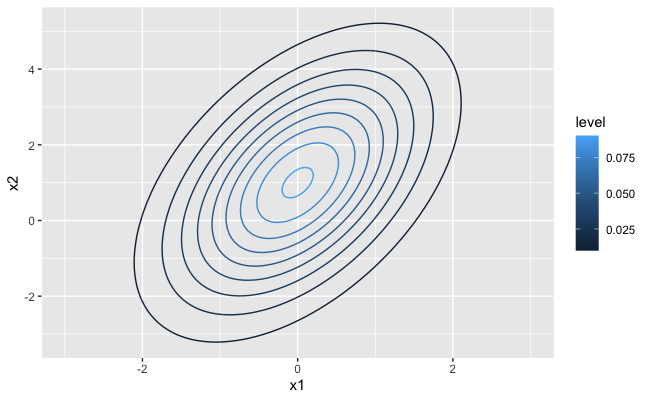
ここで、$x_2=3$が観測されたとします。(図の赤線)
# x2=3の水平線を追加
g_mvn +
geom_hline(yintercept=3, color="red", alpha=0.5)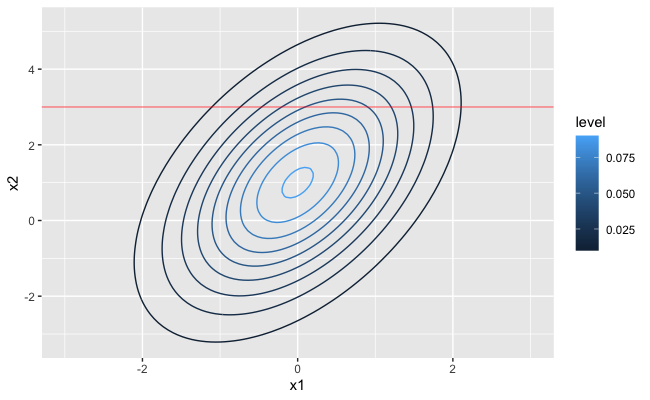
このときの$x_1$の条件つき分布を、先ほどの定理を使って実際に計算してみましょう。
$$
\begin{align}
\boldsymbol{\mu_{1|2}} & = \boldsymbol{\mu_1} + \mathbf{\Sigma_{12}}\mathbf{\Sigma_{22}^{-1}}(\boldsymbol{x_2}-\boldsymbol{\mu_2}) \\
&= 0 + \frac{1}{4}(3-1) = \frac{1}{2} \\
\mathbf{\Sigma_{1|2}} &= \mathbf{\Sigma_{11}} – \mathbf{\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}} \\
&= 1 – \frac{1\times1}{4} = \frac{3}{4}
\end{align}
$$
この正規分布の密度関数を可視化すると、このようになります。
# 条件つき分布の密度関数を可視化
g_cond = tibble(x1=x1, dens=dnorm(x1, mean=1/2, sd=sqrt(3/4))) %>%
ggplot(aes(x=x1, y=dens)) +
geom_line() +
coord_cartesian(xlim=c(min(x1), max(x1)))
g_cond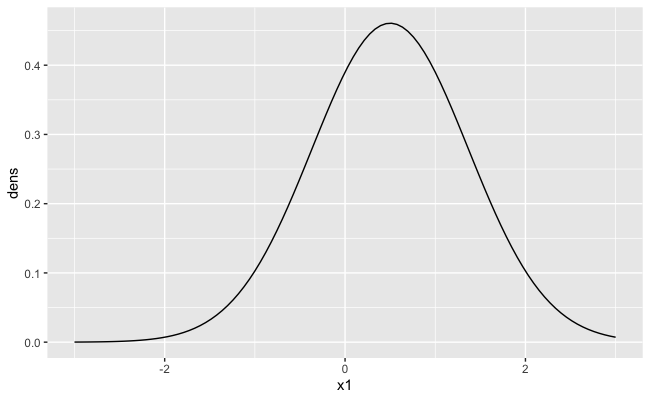
2次元正規分布$p(x_1,x_2)$の等高線と、条件つき正規分布$p(x_1|x_2=3)$の密度関数を並べてみると、確かに等高線と赤線が被っているエリアに沿って、条件つき分布の山があるように見えます。
# 並べて可視化
(
g_cond +
geom_vline(xintercept=1/2, color="black", linetype="dashed")
) / (
g_mvn +
geom_hline(yintercept=3, color="red", alpha=0.5) +
geom_vline(xintercept=1/2, color="black", linetype="dashed")
)
まとめ
今回は、多変量正規分布の条件つき分布における平均・分散の導出と、簡単な例を用いた可視化をご紹介しました。
次回は、潜在変数$x$と観測値$y$の間に線形関係がある場合の、$x|y$の条件つき分布の導出を紹介したいと思います。
参考: