PPLでの状態空間モデルの実装
状態空間モデルをMCMCで実行する機会がちょいちょいあるのですが、そんな時は使い慣れたrstan、もしくはcmdstanrをずっと使用してきました。(たまにGoogleの開発したRのライブラリ“bsts”も使用)
ただ、stanはMCMCが高速というわけではないので、試行錯誤が必要な場面ではその計算スピードに悩まされることもありました。
stan以外のPPLだと、PyMCやNumpyro、PyroなどPython上で動かすものたちがメジャーになってきており、それらはGPUを使った並列化によるMCMC高速化が可能だったりします。
なので、「stanでなくそれらを使えば、状態空間モデルのMCMCももっと早く終わるのでは?」と考えてはいたのですが、ググっても状態空間モデルの実装例が見つからず、また状態空間モデルの『第$t$期のパラメータが第$t-1$期のパラメータに依存する』という逐次的な構造は、並列化の恩恵にあずかれないのでは?という疑問もあったので、不満はありつつもずっとstanを使ってきてました。
ただ、最近Numpyroの公式ページを覗いてみると、この逐次的な構造を取り扱える関数を発見したので、stanより高速なMCMCが状態空間モデルで可能かトライしてみました。今回の記事では、その実装内容と結果についてご紹介します。
ちなみに、stanでの状態空間モデルについては以下のページが大変参考になります。
また、別のPPLであるTensorflow Probabilityでは、bstsのように簡単に状態空間モデルが実装できるモジュールがあるようです。ただ、私がTensorflowの実装経験が皆無なのと、非線形・非ガウスの状態空間モデルが実装できるか不明だったので、こちらについては今回は触れていません。興味がある方はこちらをご参照ください。
Numpyroについては以前ブログで取り上げたこともあり、(stanほどではないですが)実装経験が少しはあった、というのも今回Numpyroを選んだ要因です。
使用データ
今回は、”焼肉”というワードの検索推移のデータをGoogleトレンドからダウンロードして使用します。期間は2022/4/1-9/30の半年間です。
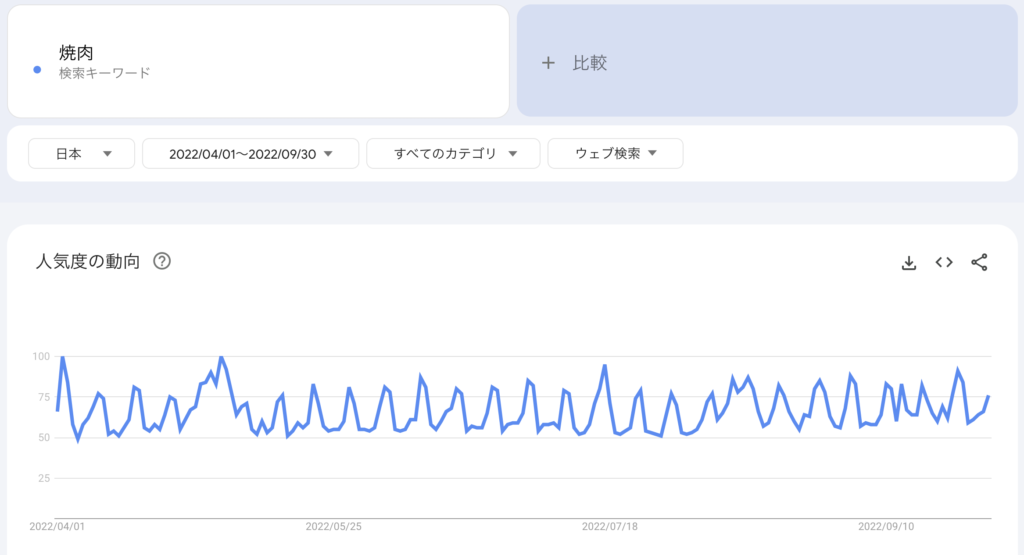
なぜ”焼肉”というワードを選んだかというと、いくつか調べたワードの中で、曜日による変動が特に顕著だったからです。
上のグラフを見ていただくと、波に分かりやすく周期性があることが分かります。細かくみると、大体土曜日に波の頂点が来ていました。この周期性も、状態空間モデルでモデリングしていこうと思います。
実行環境
今回は、M1 mac上にDocker Desktopを使って作成した仮想環境内で実行しました。ただし、m1のアーキテクチャがARM64なため、jaxlibをpip installではなくソースからインストールする必要がありました。(こちらを参考にしました)
このビルドに1〜2時間かかったので、可能ならamd64環境を使ってpip installすることをオススメします。
また、最初は前回のNumpyro投稿と同様、Google Colaboratory ProによるGPU環境を使用していました。しかし試しているうちに、Colab ProのGPU環境よりも普通のCPU環境のほうが計算が何倍も速くなることに気づきました。この原因は正直よく分からないのですが、先ほど述べたような状態空間モデルの逐次的な構造のためかな?と睨んでいます。
モデル式
今回実装するモデルは、以下の式で表現します。
$$
\begin{align}
\begin{cases}
y_t = \mathbf{A} \boldsymbol{\mu_t} + \delta_t \\
\boldsymbol{\mu_t} = \mathbf{B} \boldsymbol{\mu_{t-1}} + \boldsymbol{\varepsilon_t}
\end{cases}
\end{align}
$$
各パラメータの定義は以下です。
$$
\begin{align}
\mathbf{A} &=\begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}, \\
\mathbf{B} &= \begin{pmatrix}1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & -1 & -1 & -1 & -1 & -1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\end{pmatrix}, \\
\boldsymbol{\mu_t} &= \begin{pmatrix} \mu_{t, 0} & \mu_{t, 1} & \mu_{t, 2} & \mu_{t, 3} & \mu_{t, 4} & \mu_{t, 5} & \mu_{t, 6} & \mu_{t, 7}\end{pmatrix}^T, \\
\boldsymbol{\varepsilon_t} &= \begin{pmatrix} \varepsilon_{t, 0} & \varepsilon_{t, 1} & \varepsilon_{t, 2} & 0 & 0 & 0 & 0 & 0\end{pmatrix}^T
\end{align}
$$
$\boldsymbol{\mu_t}$の最初の2つの項は、トレンドを表現するためのローカル線形トレンドモデルのための項です。残り6つの項は、曜日による違いを表現する周期性モデルです。
$\delta_t$と$\boldsymbol{\varepsilon_t}$は適当な分布にしたがう誤差項です。ここは正規分布に設定することが多いですが、もちろん他の分布でも構いません。
上の式は少々複雑ですが、モデルをできるだけベクトルで表現することが、Numpyroでの計算高速化の肝だと思ってるのでこの形式にしました。(実際はどうかは分かりませんが…。)
状態空間モデルの実装
では実装してみます。必要なライブラリは事前にインストールしておきます。
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import arviz as az
import jax
import jax.numpy as jnp
import jax.random as random
import numpyro
import numpyro.distributions as dist
from numpyro import handlers
from numpyro.contrib.control_flow import scan
from numpyro.diagnostics import hpdi
from numpyro.infer import Predictive, init_to_feasible, init_to_median
# MCMCを4chain並列に回すための設定
numpyro.set_host_device_count(4)Googleトレンドからデータをcsvでダウンロードし、pandasで読み込みます。
df = pd.read_csv("./data/googletrends_yakiniku.csv", skiprows=[0], parse_dates=["日"])
df.rename(columns={"日": "date", "焼肉: (日本)": "value"}, inplace=True)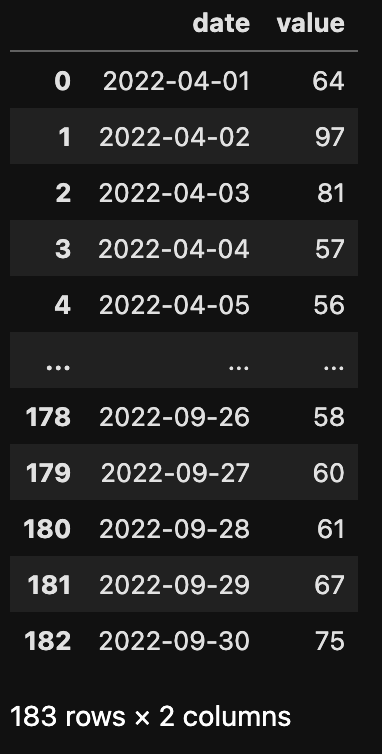
このデータをjax.numpyの配列に格納します。
y = jnp.array(df["value"].values)
N = y.shape[0]では先ほど数式で記述したモデルを、Numpyroの記法で定義します。
def model(obs=None):
# 事前分布:状態変数の標準偏差
sigma_mu0 = numpyro.sample("sigma_mu0", dist.LogNormal(0, 0.5))
sigma_mu1 = numpyro.sample("sigma_mu1", dist.LogNormal(0, 0.5))
sigma_mu2 = numpyro.sample("sigma_mu2", dist.LogNormal(1, 1))
# 事前分布:観測値の標準偏差
sigma_y = numpyro.sample("sigma_y", dist.LogNormal(1, 1))
# 状態変数の初期値(=第0期の値)
mu_0 = numpyro.sample(
"mu_0", dist.Normal(jnp.zeros([8]), 10 * jnp.ones([8])).to_event(1)
)
# 状態変数の誤差項
# 誤差項が存在するのは最初の3つだけ
eps_mu0 = numpyro.sample(
"eps_mu0", dist.Normal(jnp.zeros([N]), sigma_mu0 * jnp.ones([N])).to_event(1)
)
eps_mu1 = numpyro.sample(
"eps_mu1", dist.Laplace(jnp.zeros([N]), sigma_mu1 * jnp.ones([N])).to_event(1)
)
eps_mu2 = numpyro.sample(
"eps_mu2", dist.Normal(jnp.zeros([N]), sigma_mu2 * jnp.ones([N])).to_event(1)
)
# 残りの5つは0で固定なので、0で埋める
eps_mu_add = jnp.concatenate(
[jnp.stack([eps_mu0, eps_mu1, eps_mu2], axis=1), jnp.zeros([N, 5])],
dtype=float,
axis=1,
)
# 係数行列
A = jnp.array([1.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0])
B = jnp.array(
[
[1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0],
[0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0],
]
)
# 状態変数の時系列変動を定義
def transition(mu_prev, eps):
mu_curr = jnp.matmul(B, mu_prev) + eps
return mu_curr, mu_curr
_, mu = scan(transition, mu_0, eps_mu_add, length=N)
numpyro.deterministic("mu", mu)
# 観測値yの平均
mean_y = jnp.matmul(mu, A)
numpyro.deterministic("mean_y", mean_y)
# yの分布
y_sample = numpyro.sample(
"y_sample", dist.Normal(mean_y, sigma_y * jnp.ones([N])).to_event(1), obs=obs
)
return y_sampleポイントは、transition関数で状態空間モデルの状態方程式を定義し、状態変数の逐次構造をscan関数で表現することで、状態変数muを取得している点です。
このscan関数の挙動について、申し訳ないですが私の語彙力では十分な説明が出来ないので、こちらのjaxのscan関数に関するドキュメントを参照してください。。。
また、パラメータeps_mu1のしたがう分布としてラプラス分布を設定しています。これは、ラプラス分布が正規分布より尖っているかつ裾が厚い分布であることを利用し、『トレンドの傾きは基本ほぼ変化しないが、いざとなれば大きく変化できる』という設定をモデルに組み込んでいます。(Prophetと同じ考え方です)
このモデルブロックがうまく定義できているか確認するため、このモデルから事前予測サンプルを生成します。
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
# 事前予測を実施
prior_predictive = Predictive(model, num_samples=1000)
prior_predictions = prior_predictive(rng_key_)
# yの平均とHDI区間を取得
prior_median = jnp.median(prior_predictions["y_sample"], axis=0)
prior_hdi = hpdi(prior_predictions["y_sample"], prob=0.95)
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(df["date"], df["value"], "o")
ax.plot(df["date"], prior_median)
ax.fill_between(
df["date"], prior_hdi[0], prior_hdi[1], alpha=0.3, interpolate=True
)
fig.show()事前予測、つまりデータを与えず事前分布のみからサンプルを生成しているため、分散が尋常じゃなく大きいですが、意図通りの挙動をしていそうなことが確認できました。
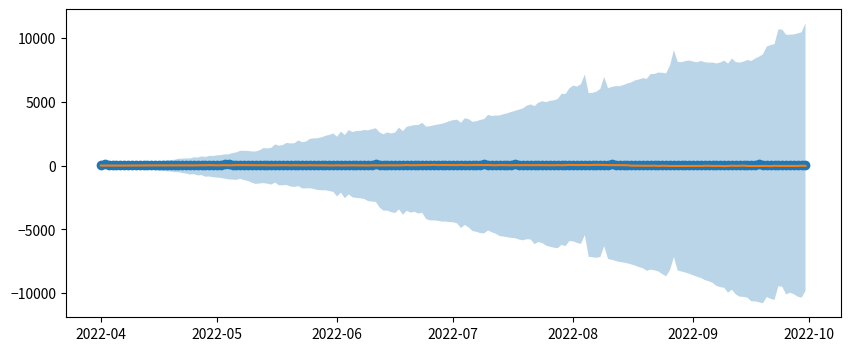
事前予測サンプルでの状態変数の挙動も確認してみます。こちらも問題なさそうです。
# 状態変数mu_0, mu_1, mu_2の事前予測平均を可視化
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
axes = axes.flatten()
axes[0].plot(df["date"], jnp.median(prior_predictions["mu"][:, :, 0], axis=0))
axes[1].plot(df["date"], jnp.median(prior_predictions["mu"][:, :, 1], axis=0))
axes[2].plot(df["date"], jnp.median(prior_predictions["mu"][:, :, 2], axis=0))
axes[0].set_title(r"$\mu_{t, 0}$")
axes[1].set_title(r"$\mu_{t, 1}$")
axes[2].set_title(r"$\mu_{t, 2}$")
fig.show()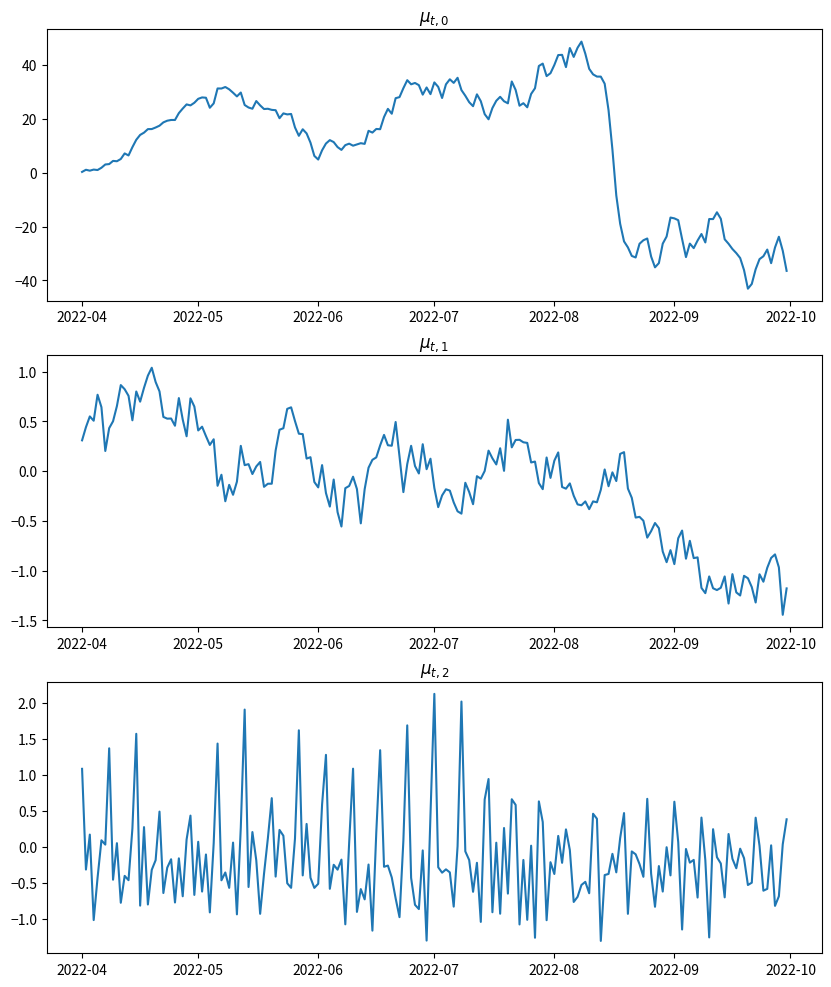
では、観測値$y_t$を与えてMCMCによる推論を実行します。私の環境では、以下の設定で約10分かかりました。
rng_key, rng_key_ = random.split(rng_key)
kernel = numpyro.infer.NUTS(model, init_strategy=init_to_median(), max_tree_depth=20)
# progress_bar=Falseにすると、計算スピードがアップするらしい
mcmc = numpyro.infer.MCMC(
kernel,
num_warmup=1000,
num_samples=2000,
thinning=1,
num_chains=4,
progress_bar=True,
)
mcmc.run(rng_key_, obs=y)各パラメータに関する結果の要約を計算し、r_hatが高い順に並べてみます。一番大きいパラメータでr_hatが1.09なので、MCMCは収束したと言えそうです。
df_summary = az.summary(mcmc)
df_summary.sort_values("r_hat", ascending=False)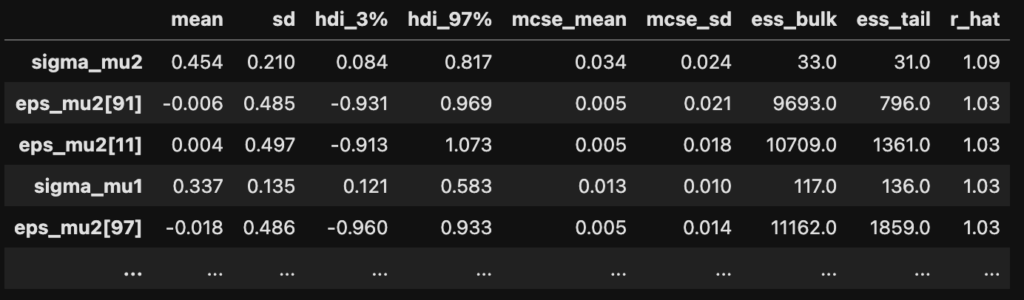
MCMCサンプルを取得します。
samples = mcmc.get_samples()そして、この得られたサンプルを用い、$y_t$の事後予測サンプルを生成します。
rng_key, rng_key_ = random.split(rng_key)
predictive = Predictive(model, samples)
predictions = predictive(rng_key_)["y_sample"]y_sampleから事後平均と95%HDIを計算し、観測値と一緒にプロットしてみます。予測値は、大まかには観測値を追えているようです。
mean_y = jnp.mean(predictions, axis=0)
hdi_y = hpdi(predictions, 0.95)
fig, ax = plt.subplots(figsize=(20, 5))
ax.plot(df["date"], df["value"], "o", color="black")
ax.plot(df["date"], mean_y, color="#007199")
ax.fill_between(df["date"], hdi_y[0], hdi_y[1], alpha=0.3, facecolor="#007199")
fig.show()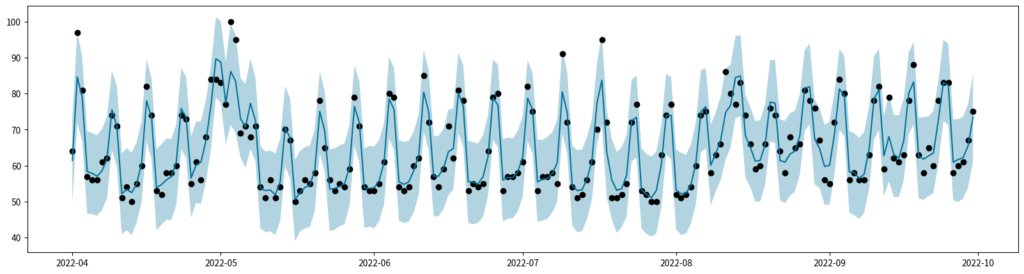
状態変数$\mu_t$の推移もチェックしてみましょう。上段がトレンドの値$\mu_{t,0}$、中段がトレンドの傾き$\mu_{t,1}$、下段が周期性$\mu_{t,2}$の推移です。
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
axes = axes.flatten()
samples_mu = samples["mu"]
mean_mu = jnp.mean(samples_mu, axis=0)
hdi_mu = hpdi(samples_mu, prob=0.95)
axes[0].plot(df["date"], mean_mu[:, 0])
axes[0].fill_between(df["date"], hdi_mu[0, :, 0], hdi_mu[1, :, 0], alpha=0.3)
axes[1].plot(df["date"], mean_mu[:, 1])
axes[1].fill_between(df["date"], hdi_mu[0, :, 1], hdi_mu[1, :, 1], alpha=0.3)
axes[2].plot(df["date"], mean_mu[:, 2])
axes[2].fill_between(df["date"], hdi_mu[0, :, 2], hdi_mu[1, :, 2], alpha=0.3)
axes[0].set_title(r"$\mu_{t, 0}$")
axes[1].set_title(r"$\mu_{t, 1}$")
axes[2].set_title(r"$\mu_{t, 2}$")
fig.show()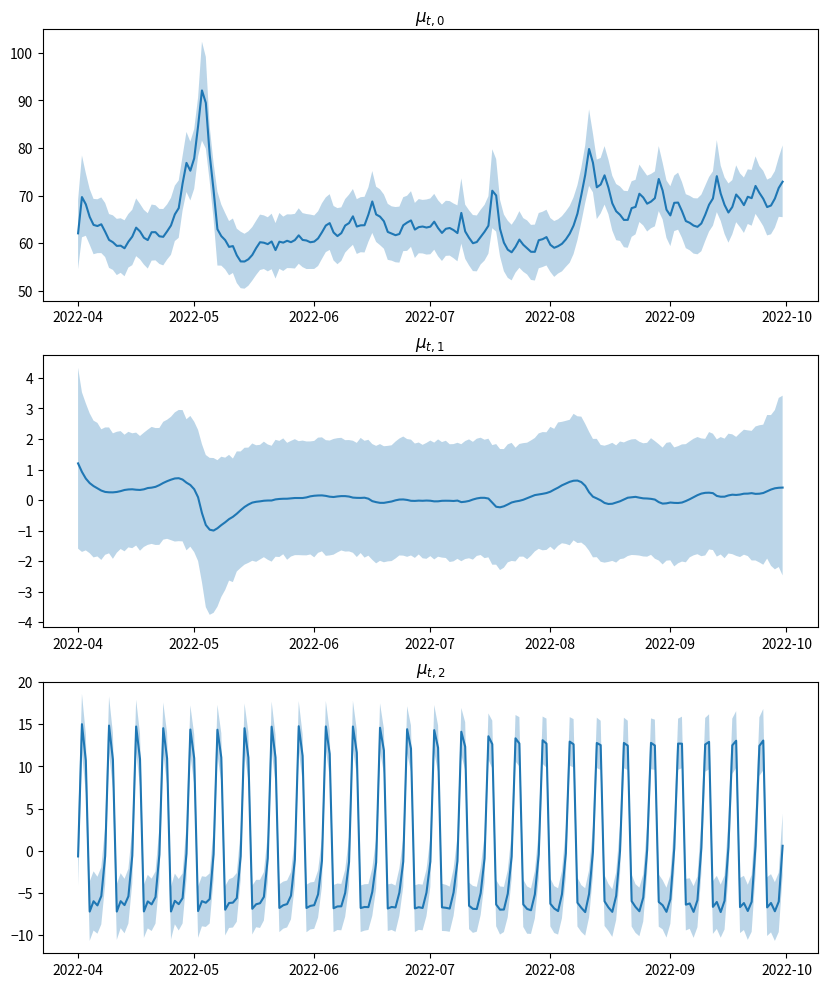
以上で各パラメータの推定は終わりです。
では、得られたパラメータのサンプルを使い、将来予測を行ってみます。まず以下のように、将来値を生成するための関数を定義します。
def forecast(samples, N_forecast):
# MCMCサンプルの数
n_samples = samples["sigma_mu0"].shape[0]
# 状態変数の誤差項
eps_mu0 = numpyro.sample(
"eps_mu0",
dist.Normal(
jnp.zeros([N_forecast, 1]), samples["sigma_mu0"] * jnp.ones([N_forecast, 1])
),
)
eps_mu1 = numpyro.sample(
"eps_mu1",
dist.Laplace(
jnp.zeros([N_forecast, 1]), samples["sigma_mu1"] * jnp.ones([N_forecast, 1])
),
)
eps_mu2 = numpyro.sample(
"eps_mu2",
dist.Normal(
jnp.zeros([N_forecast, 1]), samples["sigma_mu2"] * jnp.ones([N_forecast, 1])
),
)
eps_mu_add = jnp.concatenate(
[
jnp.stack([eps_mu0, eps_mu1, eps_mu2], axis=2),
jnp.zeros([N_forecast, n_samples, 5]),
],
dtype=float,
axis=2,
)
# 係数行列
A = jnp.array([1.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0])
B = jnp.array(
[
[1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0],
[0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0],
]
)
# 状態方程式を関数で定義
def transition(mu_prev, eps):
mu_curr = jnp.matmul(B, mu_prev) + eps
return mu_curr, mu_curr
# 将来の状態変数を生成
init_mu = samples["mu"][:, -1, :].T
_, mu = scan(transition, init_mu, jnp.swapaxes(eps_mu_add, 1, 2), length=N_forecast)
# 将来の観測値を生成
mean_y = jnp.matmul(A, mu)
y_sample = numpyro.sample(
"y_sample",
dist.Normal(mean_y, samples["sigma_y"] * jnp.ones([N_forecast, 1])).to_event(1),
)
return y_sampleこの関数と得られたMCMCサンプルを使い、将来値を生成した後、その事後平均と95%HDI区間を計算します。
# 将来値を予測する日数
N_forecast = 14
rng_key, rng_key_ = random.split(rng_key)
samples_y_forecast = handlers.seed(forecast, rng_seed=rng_key_)(
samples, N_forecast
)
mean_y_forecast = jnp.mean(samples_y_forecast, axis=1)
hdi_y_forecaset = hpdi(samples_y_forecast.T, 0.95)結果を可視化してみます。予測区間がかなり広いので、精度面では恐らく良くない結果になるでしょうが、今回は実装紹介がメインなのでこれで良しとしましょう。
fig, ax = plt.subplots(figsize=(20, 5))
ax.plot(
jnp.arange(N + N_forecast),
jnp.concatenate([df["value"].values, jnp.repeat(jnp.nan, N_forecast)]),
"o",
color="black",
)
ax.plot(
jnp.arange(N + N_forecast), jnp.concatenate([mean_y, mean_y_forecast]), color="#007199"
)
ax.fill_between(
jnp.arange(N + N_forecast),
jnp.concatenate([hdi_y[0], hdi_y_forecaset[0]]),
jnp.concatenate([hdi_y[1], hdi_y_forecaset[1]]),
alpha=0.3,
facecolor="#007199",
)
fig.show()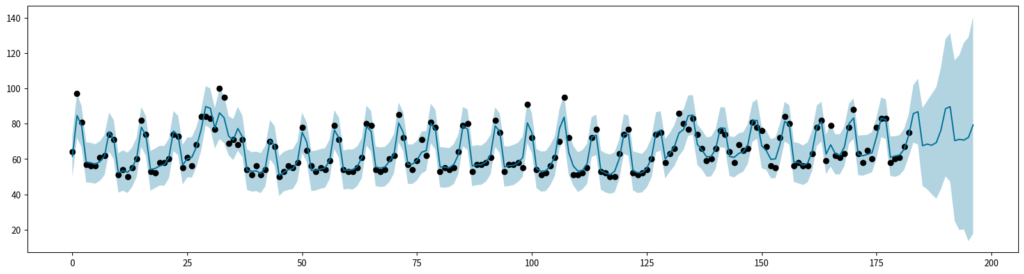
以上でNumpyroによる状態空間モデルの実行は終わりです。
Stanより高速なのか?
上記のNumpyroによる実装となるべく同じ設定で、cmdstanrでもMCMCを実行してみました。すると、stanの計算時間は約7分とNumpyroよりも短くなりました。。。もちろん実行環境やシード次第で結果は変わるかもしれませんが、今回の結果だけみると、Numpyroは速度面ではstanに負けてしまいました。
ただ、Numpyroのメリットとして、事前予測・事後予測がかなり簡単に実行できる点が挙げられます。stanでこれらを行おうとすると、stanファイルの書き方を結構工夫しないといけないと思います。(generated quantitiesブロックとか)
また、stanの場合はstanファイルを書き換えるたびにコンパイルに数十秒かかるのですが、これが何回も試行錯誤する際には地味にストレスになります。Numpyroのコンパイルは体感2~3秒で終わるので、ここにもNumpyroのメリットがあると考えます。
まとめると、「お手軽さで言えばNumpyroに軍配が上がる」というのが個人的な感想です。また階層ベイズのような逐次構造がない場合は、並列化により速度でもNumpyroが圧勝すると思われるので、自分がMCMCを回す際は(記法に慣れさえすれば)Numpyroを選ぶケースがほとんどになってくるのかなと思いました。
参考: