Numpyroで主成分分析を実装してみる

みなさんは普段、どのようにベイズモデリングを実装されていますか？

アカデミックの方や理論・プログラミングに明るい人は「自分でMHアルゴリズムなどMCMCを一から実装している」という選択肢をとられているかもしれません。

が、私のようなビジネスにベイズモデリングを応用している立場の人間は、stanに代表される確率的プログラミング言語(PPL)を使っている方がほとんどではないかな、と思います。

PPLにはstan以外にもいろいろあり、2022年5月に発売された『Pythonではじめるベイズ機械学習入門』では、Pythonにて使用できる以下のPPLを使った様々な手法の実装方法が、幅広く解説されています。

PyMC3
Pyro
Numpyro
Tensorflow Probability

その中の一つとして、PyMC3を使った主成分分析の実装方法が取り上げられていたのですが、今回のブログではPyMC3をNumpyroに置き換えて主成分分析(PCA)を実装してみたいと思います。

Numpyroとは？

NumpyroはUberが開発したPPLで、統計モデルを簡単に記述できると同時に、GPUを使った計算の高速化を実現しています。

同じくUberが開発しているPyroと文法が似通っているのも特徴です。では「NumpyroとPyroの違いは何か？」というと、以下のような差異があります。

Numpyro → MCMCに特化したPPL
Pyro → 変分推論に特化したPPL

また、Numpyroはまだ開発途中(2020年6月現在)ですので、今後文法が一部変更される可能性があります。本記事のコードもバージョンによっては動かなくなる可能性がありますのでご承知おきください。

ちなみに、以前ブログにてPyroを使った混合ベルヌーイモデルの実装方法を取り上げているので、ご興味のある方は是非そちらもご覧ください。

Pyroで混合ベルヌーイによるクラスタリングをやってみる

主成分分析(PCA)の確率モデル表現

主成分分析(PCA)の計算方法を知っている方は、「あれ、PCAって確率とか関係あったっけ？」と思われるかもしれません。実は、PCAは潜在変数を使った確率モデルとして定義することもできます。

具体的に数式で表してみます。観測されたデータ$x_n$の次元数を$D$とし、これを$D$より少ない次元数$K$の潜在変数$z_n$に縮約することを考えます。このとき、式は以下になります。

$$
x_n = \mu + Wz_n + \varepsilon_n,
$$

ただし、$z_n$と$\varepsilon_n$はそれぞれ$z_n \sim N(0, I)$、$\varepsilon_n \sim N(0, \sigma^2 I)$という正規分布にしたがいます。このようにPCAに確率的な表現を与えたモデルのことを確率的主成分分析(PPCA)といいます。

このPPCAでは、データ$x_n$が生成されるステップを以下のように考えています。

$K$次元のデータ$z_n$が標準正規分布から生成される
$z_n$に$D\times K$の行列$W$をかける
さらに$\mu$とノイズ$\varepsilon_n$を足すことで、$D$次元の観測データ$x_n$がつくりだされる

個人的には、通常のPCAの説明における「分散が最大になるように射影を〜」とか「共分散行列の固有値が〜」とかいう説明をされるより、上記のPPCAのほうがしっくりきますし、PPLを使えば実装もカンタンです。

もちろん、従来のPCAのほうがしっくりくる方は、別にPPCAのほうを無理に使う必要はありません。scikit-learnとかでカンタンに実行できるので、一から自分で実装する必要もないですしね。

では確率モデルを使うメリットは何なのでしょうか？『Pythonではじめるベイズ機械学習入門』では特にメリット・デメリットという観点でこのPPCAを紹介しているわけではなく、行列分解モデルの一種として、協調フィルタリングと同列にこのモデルを紹介しているだけです。

なのでここからはあくまで私個人の考えになるのですが、PPCAのメリットは因子分析と主成分分析を同じフレームワークで扱えるところにあるのではないかな、と思っています。

というのも、Murphyの『Machine Learning』によると、先述の確率モデルにおける$\varepsilon_n \sim N(0,\sigma^2I)$の$\sigma^2I$を、より一般化した共分散行列$\Psi$に置き換えたものが因子分析と呼ばれているモデルになります。
(ただし、詳細は省きますが$\Psi$は対角行列でないといけません)

主成分分析と因子分析の違いについて巷にはいろんな説明がありますが、確率モデルで表記すると「主成分分析は因子分析の特殊ケース」ということになります。

ちなみに、PPCAにおいて$\sigma \rightarrow 0$にし、$W$が直交行列になるよう制約をかけると、PPCAは従来のPCAと同一になります。

Numpyroで実装

ではNumpyroでPPCAを実装してみます。今回も『Pyroで混合ベルヌーイによるクラスタリングをやってみる』と同様にMNISTを使用します。『ゼロから作るディープラーニング』のコードを参考に、事前にGoogleドライブへMNISTデータをダウンロードしておきます。

環境はGoogle Colaboratoryを使います。ちなみにPyroもNumpyroもGPUによる計算高速化が可能ですので、Colaboratoryの設定でGPUをオンにすることを推奨します。
私はこの計算のために、より高性能なGPUが使えるColab Pro(有料)を使い始めました。

まず、Numpyroをインストールします。

!pip install numpyro

必要なライブラリを読み込みます。事前にGoogleドライブをマウントしてください。(方法はこちら)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import sys
#『ゼロから作るディープラーニング』のmnist.pyファイルが置いてあるドライブ上のパスを指定
sys.path.append('Path')
from mnist import load_mnist

import jax
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist

データとして最初の1,000個を使います。

train, test = load_mnist(normalize=False, flatten=False, one_hot_label=False)

data = np.squeeze(train[0][0:1000] / 256).copy()
segment = train[1][0:1000].copy()

最初の15個を可視化してみます。

fig, axes = plt.subplots(3, 5, figsize=(10, 5))

for i, ax in enumerate(axes.flatten()):
    ax.imshow(data[i])
fig.show()

Numpyroに突っ込む準備として、データをjax.numpyの配列に変換し、潜在変数の次元数などを設定します。

x = jnp.array(data.reshape(data.shape[0], -1))

# 潜在変数zの次元数
K = 10
# 元データの行数
N = x.shape[0]
# 元データの列数
D = x.shape[1]

print(f'nrow : {N}')
print(f'ncol : {D}')
print(f'dim of latent variable : {K}')

#nrow : 1000
#ncol : 784
#dim of latent variable : 10

Numpyroでモデルを定義します。$W$や$\sigma$に事前分布を設定するのですが、今回は『Pythonではじめるベイズ機械学習入門』で紹介されているものではなく、書籍で引用されているBishopの論文『Bayesian PCA』を参考に、$W$の各行$k(1 \leq k \leq K)$が平均0、標準偏差$\alpha_k$の正規分布にしたがうという設定にします。

こうすることで、潜在変数の次元数を$K$に設定した際に、$K$の中でも情報量が多い要素/少ない要素のような濃淡をつけることができます。

def model(obs):
    # alpha : Wの各列の標準偏差
    alpha = numpyro.sample("alpha", dist.Exponential(rate=jnp.ones([K])).to_event(1))
    # W : ｚにかかる行列
    W = numpyro.sample("w", dist.Normal(jnp.zeros([K, D]), jnp.repeat(alpha, D, axis=0).reshape(K, D)).to_event(2))
    # xの標準偏差
    sigma = numpyro.sample("s", dist.HalfCauchy(scale=1))
    
    # 各データに対してzとxの分布を定義
    with numpyro.plate("plate", N):
        # z : 潜在変数
        z = numpyro.sample("z", dist.Normal(jnp.zeros([K]), jnp.ones([K])).to_event(1))
        # xの平均
        mean = jnp.matmul(z, W)
        # データxの分布
        x = numpyro.sample("x", dist.Normal(loc=mean, scale=sigma * jnp.ones([D])).to_event(1), obs=obs)

ではMCMCを実行します。今回はwarmupを1000、warmup後のiteration数を10000、間引き(thinning)を5に設定しました。chain数ですが『Pythonではじめるベイズ機械学習入門』でも解説されているように、$W$や$z$の符号がchainごとに逆転してしまう可能性があるため、chain=1に設定しています。

計算時間は無償版だと1時間以上かかってしまいましたが、有料版のCobal Proであれば10分ほどで終わりました。

kernel = numpyro.infer.NUTS(model)
mcmc = numpyro.infer.MCMC(kernel, num_warmup=1000, num_samples=10000, thinning=5, num_chains=1)

mcmc.run(jax.random.PRNGKey(1), obs=x)

MCMCの結果を取り出します。

samples = mcmc.get_samples()
samples.keys()
#dict_keys(['alpha', 's', 'w', 'z'])

1番目のデータに対応する$z$のトレースプロットを見てみます。ちょっと収束状況がビミョーですが、一旦この結果を使うことにします。

fig, axes = plt.subplots(2, 5, figsize=(20, 7), sharey=True)
axes = axes.flatten()
for k in range(K):
    axes[k].plot(samples["z"][:, 0, k])
    axes[k].set_title(f'z[{k}] of first sample')
fig.show()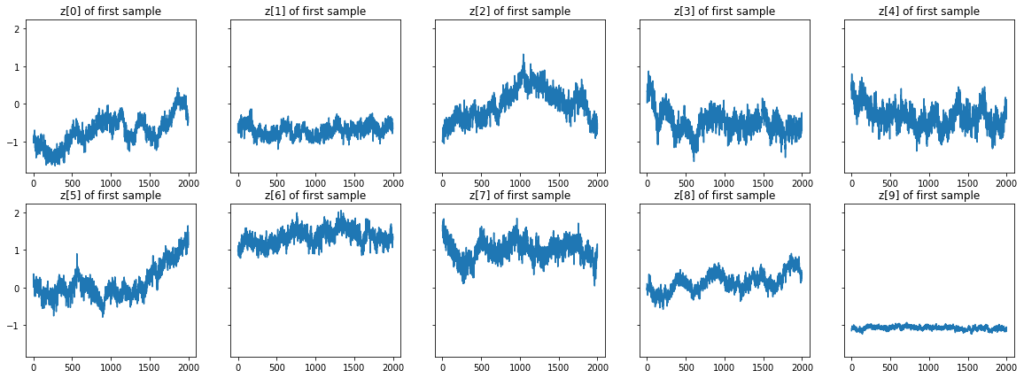

結果を使いやすくするために、MCMCサンプルから中央値を取り出し、この中央値を推定結果として扱うことにします。

まず$W$の推定値を取り出し、結果を可視化してみます。グラフを見ると、間が途切れ途切れになっていることが分かります。この部分はMNISTの画像において、ほとんど白紙である端っこの部分に対応しています。

W_med = np.array(jnp.median(samples["w"], axis=0))
# 可視化のために、W_medを変形し7840×3の行列にする
xx, yy = np.meshgrid(np.arange(1, D+1), np.arange(1, K+1))
W_plt = np.c_[xx.flatten(), yy.flatten(), W_med.flatten()]

fig, ax = plt.subplots(figsize=(15, 7))
ax.scatter(W_plt[:, 0], W_plt[:, 1], s=100*(W_plt[:, 2]**2), c=["b" if x>=0 else "r" for x in W_plt[:, 2]])
fig.show()

続いて$z$の推定値を取り出します。中央値を計算し、後の処理のためにpandasのデータフレームに格納します。

z_med = np.array(jnp.median(samples["z"], axis=0))

list_z_med = list()
for i in range(K):
    df_z = pd.DataFrame(z_med[segment==i, :])
    df_z['segment'] = str(i)
    df_z = df_z.set_index('segment').stack().reset_index()
    df_z = df_z.rename(columns={'level_1': 'dim', 0: 'value'})
    list_z_med.append(df_z)
    del df_z

df_z_med = pd.concat(list_z_med, axis=0)

1,000個の$z$の推定値を、「元々のデータが0~9のどの数字が書かれていたか」によって分割し、それらの中で$z$の推定値の平均をとって可視化してみます。この結果を解釈することはできませんが、色が結構バラバラなので0~9の数字間で何かしらの違いを持った10次元の特徴量を抽出できてはいそうですね。

fig, axes = plt.subplots(2, 5, figsize=(15, 5))
axes = axes.flatten()

l_z_plt = list()

for s in range(10):
    z_plt = df_z_med[df_z_med['segment']==str(s)].groupby('dim', as_index=True)['value'].mean().values
    l_z_plt.append(z_plt)

    axes[s].imshow(z_plt.reshape(2, 5))
    axes[s].set_title(f'{s}')
    del z_plt
fig.show()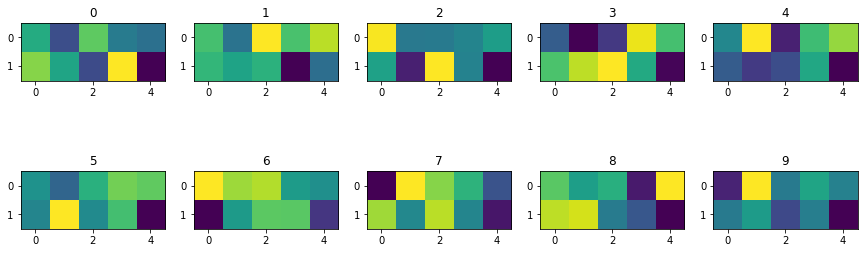

では、これまで見てきた$W$の推定値と$z$の推定値を掛け合わせ、元データを復元してみましょう。結果を見る限り、10次元でも元の数字をまあまあ復元できるレベルの特徴を捉えきれていることが分かりますね。

fig, axes = plt.subplots(2, 5, figsize=(15, 7))
axes = axes.flatten()
for s in range(10):
    axes[s].imshow(np.matmul(df_z_med[df_z_med['segment']==str(s)].groupby('dim', as_index=True)['value'].mean().values, W_med).reshape(28, 28))
    axes[s].set_title(str(s))
fig.show()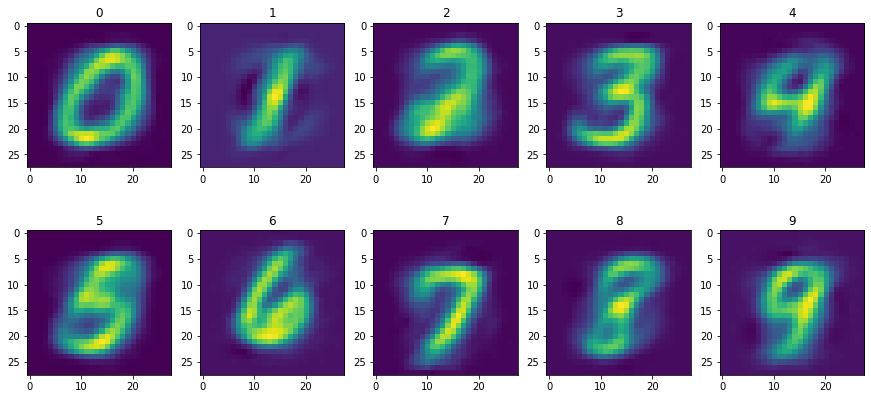

最後に

今回は、NumpyroによるPCAを実装してみました。

PPLによってベイズモデリングが簡単に実装できはするのですが、実はNumpyroを使い慣れていなかったために、コーディング時にエラーにかなり苦しめられました…。

『Pythonではじめるベイズ機械学習入門』を参考に、主成分分析のNumpyroでの実装を試みて4日目。
やっとエラーなしでMCMCが回ってくれた…。(回っただけで意図した挙動になってるかは不明)
— ぱぐみ@ベイジアン (@pagumi_bayesian) June 26, 2022

原因はbatch_shapeとevent_shapeをうまく設定できていなかったことでした。この辺は『Pythonではじめるベイズ機械学習入門』が大変参考になりました。

PryoやNumpyro、Tensorflow ProbabilityなどのPPLは、日本語の文献が全然ないのが現状ですので、Pythonでベイズモデリングする場合はこの本が必須と言っても過言ではないと思います。

あと、Colab Proの計算スピードを一度経験すると、もう無料版には戻れません…。

Numpyroとは？

主成分分析(PCA)の確率モデル表現

Numpyroで実装

最後に

コメントする コメントをキャンセル

コメントするコメントをキャンセル