前回の記事(『Numpyroで主成分分析を実装してみる』)では、確率的プログラミング言語(PPL)の一種であるNumpyroを使って、MCMCによる確率的主成分分析(PPCA)の実装方法を紹介しました。
今回は、PPCAと同じ次元削減の手法のひとつである非負値行列分解(NMF)を、PPLの一種であり、Numpyroの親戚であるPyroを使って実装してみます。
非負値行列分解(NMF)とは?
サイズが$D \times N$であり、中の数値が全て0以上の行列$X$を考えます。これを$D \times K$の行列$W$と、$K \times N$の行列$H$を使い、$X$を2つの行列の積で近似する手法がNMFです。
($W$と$H$の中身も全て非負値)
$$
X \approx WH
$$
この手法の利点は、$K$の値を$D$や$N$よりも小さく設定することで、元データの情報をなるべく残したまま、そのサイズを大幅に落としたパラメータに縮約できる点です。
例えば、$X$のサイズが$100 \times 100$であるとします。この行列の要素数は$100 \times 100=10,000$となります。
これを$K=5$に設定することで、$W$は$100 \times 5=500$、$H$は$5 \times 100=500$、トータルで$500 + 500 = 1,000$となります。つまり、情報量を可能な限り残しつつ、データサイズを10分の1に落とすことができます。
NMFのメリット
NMFの使い所をご紹介するために、例としてPOSデータやECサイトから得られるアイテム×ユーザーの購買数量データを考えます。
数量なので、当然値は全て非負値(0以上の整数値)となります。
また、アイテム数もユーザー数も何千~何万とあることが多いので、とあるアイテムを買ったユーザー・買ってないユーザーの数を比較すると、基本的に買ってないユーザーの方が圧倒的に多いです。そのため、購買データは基本的にほとんどの値が0となっている、いわゆるスパースなデータとなっています。
こうなると、購買数量データ$X$の$D \times N$要素のほとんどが情報量0であり、データサイズが大きいにもかかわらず、そのまま活用しても示唆のある結果を得づらいです。
そこで、以下のようにNMFを使うことで、サイズを大幅に落としつつ、意味のある情報だけを抽出することができます。
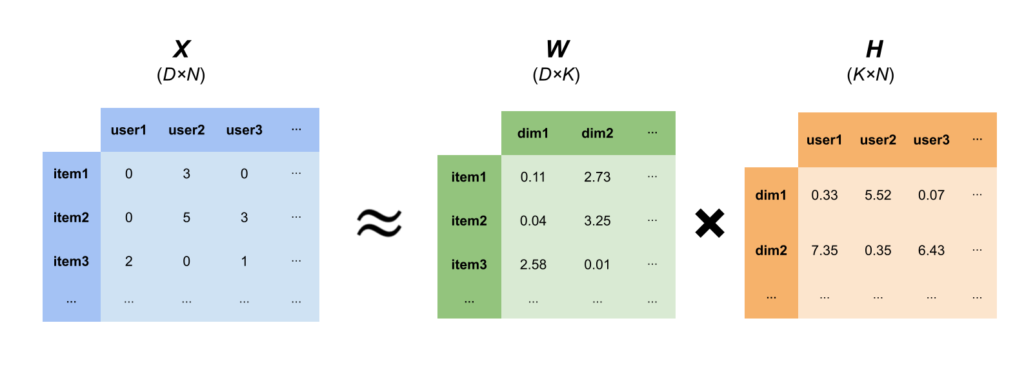
NMFの他のメリットとして、上記のような$W$や$H$を使ってアイテムやユーザー間の類似度を測ることができます。例えば、上記の$W$の中身を見ると、item1とitem2は中の数値の大きさが比較的近いため、同じような買われ方をされている→item1とitem2は比較的似たカテゴリーの商品である、という見方をすることができます。同様に$H$を見ると、user1とuser3が似ているため、この2人は同じような買い方をしているユーザーであることが予想されます。
この$W$と$H$を使うことで、アイテムやユーザーのクラスタリングをすることができます。k-meansのようなクラスタリングの手法を使ってもよいですし、シンプルに一番大きい次元がどれかでグルーピングするという方法でもいいです。(例:dim1が一番大きい→クラスター1)
またNMFには主成分分析のような他の次元縮約の手法にない、NMF独自のメリットも存在します。それは、非負値のみを取り扱うことで縮約の結果をより解釈しやすいという点です。この点に関しては『負の値は必要? 解釈しやすい行列分解「NMF」』という記事で、画像データにおけるNMFの例を使って以下のように説明されています。
普段、私たちはどのように顔の絵を描いているでしょうか。おそらく殆どの方が、輪郭を描いた後に目・口・鼻などのパーツを書き加えていくのではないでしょうか。この「書き加える」ことが非常に重要です。
出典:負の値は必要? 解釈しやすい行列分解「NMF」
「書き加える」ということは、数学の計算で表現すると「足し算をする」ことに他なりません。図4は同じ顔の絵を描こうとしています。「足し算のみのアプローチ」と「足し算と引き算の両方を使うアプローチ」がありますが、最終的には同じ顔を得ることができます。引き算も可能ということは「書き足す」だけでなく「書き減らす」こともできるので、人間ワザではない不思議なアプローチで顔を描くことができますね。

このように正の値のみが出てくるため、NMFは主成分分析やSVDよりも解釈しやすい結果が得られます。
NMFの確率モデル表現
NMFはPythonだとおなじみのscikit-learnを使うことでコード数行で実装できます。が、今回も確率モデル表現を行いPPLによる実装を行ってみます。
まず、データ$X$の要素は全て0以上の整数値であることを前提とします。$X$の$(d,n)$要素を$x_{dn}$とし、この$x_{dn}$がパラメータ$\lambda_{dn}$のポアソン分布にしたがうとします。
$$
x_{dn} \sim Poi(\lambda_{dn})
$$
NMFで出てくる行列$W$の第$d$行を$\boldsymbol{w_d}$、行列$H$の第$n$列を$\boldsymbol{h_n}$と表記すると、$\lambda_{dn}$は以下の式で表されます。
$$
\lambda_{dn} = \sum_{k=1}^K w_{dk}h_{kn} = \boldsymbol{w_d} \boldsymbol{h_n}
$$
$W$の各要素$w_{dk}$や$H$の各要素$h_{kn}$の事前分布には、以下のガンマ分布を使用します。
$$
w_{dk} \sim Gamma(\alpha_w, \beta_w),\ h_{kn} \sim Gamma(\alpha_h, \beta_h)
$$
ハイパーパラメータの$\alpha_w, \beta_w, \alpha_h, \beta_h$は適当な値を設定します。
Pyroでの実装:使用データセット
今回使うデータセットは、MovieLensという映画レビューのオープンデータです。こちらのサイトからml-latest-small.zipをダウンロードし、movies.csvとratings.csvをpandasで読み込み、結合・変形して以下のように行→映画タイトル、列→ユーザーIDの形式にしたものを使います。
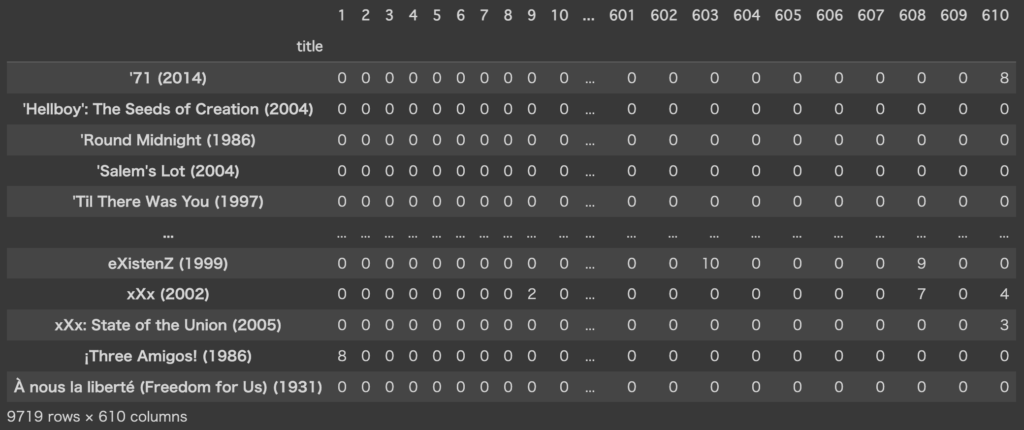
また、このレビューデータはレビュースコアが0.5~5.0の値が入っており、レビューがないセルはNaNとなっています。今回扱うモデルの都合上、NaNは0埋めし、非欠損値は2倍して整数値にしています。
このデータは行数(=映画タイトル数)が9,719、列数(=レビュー数)が610あり、要素数は全部で約600万あります。また上のデータを見てもらえれば分かる通り、ほとんどの要素が0であるスパースデータとなっています。
Pyroでの実装:Colabで実行
前回のPPCA同様、GPUによる高速計算を行うために、Google Cobaboratoryにて実行します。
まず、Pyroを使うためにpipでインストールします。ただし、PyroのバックではPyTorchが使われているのですが、Colabにあらかじめ入っているPyTorchはバージョンが新しすぎるのか原因不明のエラーが出てしまいました…。(2022年7月時点)
そのため、最初にPyTorchおよびPyTorchに依存しているライブラリをアンインストールし、その後少し古いバージョン(1.11.0)をインストールした後にPyroをインストールしました。
!pip uninstall -y torch torchvision torchtext torchaudio fastai
!pip install torch==1.11.0 pyro-ppl
次に、必要なライブラリ等をインポートします。同時にtorchがCPUでなくGPUを使うように設定します。
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
from tqdm import tqdm
import torch
from torch.distributions import constraints
import pyro
from pyro import poutine
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
torch.set_default_tensor_type(torch.cuda.FloatTensor)先ほどのレビューデータをdfという名前でpandasのデータフレームにしておき、その中身をtensor型に変形します。
x = torch.tensor(df.values.copy()).int()NMFで必要となるパラメータを設定します。今回は$K=5$に設定してみました。
# 縮約の次元数
K = 5
# 元データの行数=映画のタイトル数
D = x.shape[0]
# 元データの列数=レビュワー数
N = x.shape[1]
print(f'nrow : {D}')
print(f'ncol : {N}')
print(f'dim of latent variable : {K}')
# nrow : 9719
# ncol : 610
# dim of latent variable : 5次に、今回使う確率モデルを設定します。$W$と$H$の事前分布はガンマ分布にしました。ハイパーパラメータは、事前分布の平均が10、分散が100になるよう設定しています。
def model(obs=None):
# D×Kの行列W
W = pyro.sample("W", dist.Gamma(torch.ones(D, K), 0.1*torch.ones(D, K)).to_event(2))
# K×Nの行列H
H = pyro.sample("H", dist.Gamma(torch.ones([K, N]), 0.1*torch.ones(K, N)).to_event(2))
# Xがしたがう分布のパラメータ
lambda_x = torch.matmul(W, H)
# データxの分布
x = pyro.sample("x", dist.Poisson(lambda_x).to_event(2), obs=obs)変分推論を実行するために、このモデルをどの分布で近似するかを設定します。$W$も$H$も非負値なので、今回は各事後分布を対数正規分布で近似します。
$$
W \sim LN(\mu_W, \sigma_W^2), \quad H \sim LN(\mu_H, \sigma_H^2)
$$
最も近似精度が良い$\mu_W, \sigma_W, \mu_H, \sigma_H$を求めるのが変分推論です。
def guide(obs):
# W
loc_w_q = pyro.param("loc_w_q", torch.zeros(D, K))
scale_w_q = pyro.param("scale_w_q", torch.ones(D, K), constraint=constraints.positive)
pred_W = pyro.sample("W", dist.LogNormal(loc_w_q, scale_w_q).to_event(2))
# H
loc_h_q = pyro.param("loc_h_q", torch.zeros(K, N))
scale_h_q = pyro.param("scale_h_q", torch.ones(K, N), constraint=constraints.positive)
pred_H = pyro.sample("H", dist.LogNormal(loc_h_q, scale_h_q).to_event(2))
return pred_W, pred_Hでは変分推論を実行します。今回の設定でCobal ProのGPUで実行した場合、計算時間は約15分でした。
pyro.clear_param_store()
optimizer = pyro.optim.Adam({'lr': 0.0001, "betas": (0.95, 0.999)})
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
pyro.set_rng_seed(123)
print(f'initial loss = {svi.loss(model, guide, x)}')
loss_list = []
for _ in tqdm(range(100000)):
loss = svi.step(x)
loss_list.append(loss)Lossの推移を見ると収束しているようです。
plt.plot(loss_list)
plt.xlabel('Iter Num')
plt.ylabel('Loss')
plt.show()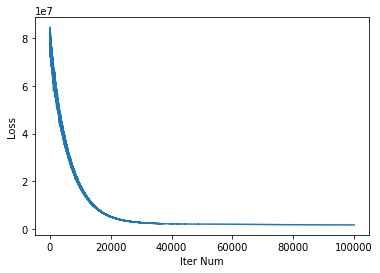
変分推論によって求めたパラメータを取得し、GPU→CPUへコピーしnumpy配列へ変換します。
loc_w_q = pyro.param('loc_w_q').to('cpu').detach().numpy()
scale_w_q = pyro.param('scale_w_q').to('cpu').detach().numpy()
loc_h_q = pyro.param('loc_h_q').to('cpu').detach().numpy()
scale_h_q = pyro.param('scale_h_q').to('cpu').detach().numpy()では、得られたパラメータを使って$W$を算出し、結果を解釈してみます。(今回は$H$の結果は見ません)
今回は$W$の推論結果として、近似事後分布の平均を使用することにします。対数正規分布の平均は、$LN(\mu,\sigma^2)$の場合$\exp(\mu + \frac{1}{2}\sigma^2)$となるので、この値を計算しDataFrame形式にします。
df_W = pd.DataFrame(np.exp(loc_w_q + 0.5*scale_w_q**2), index=df.index)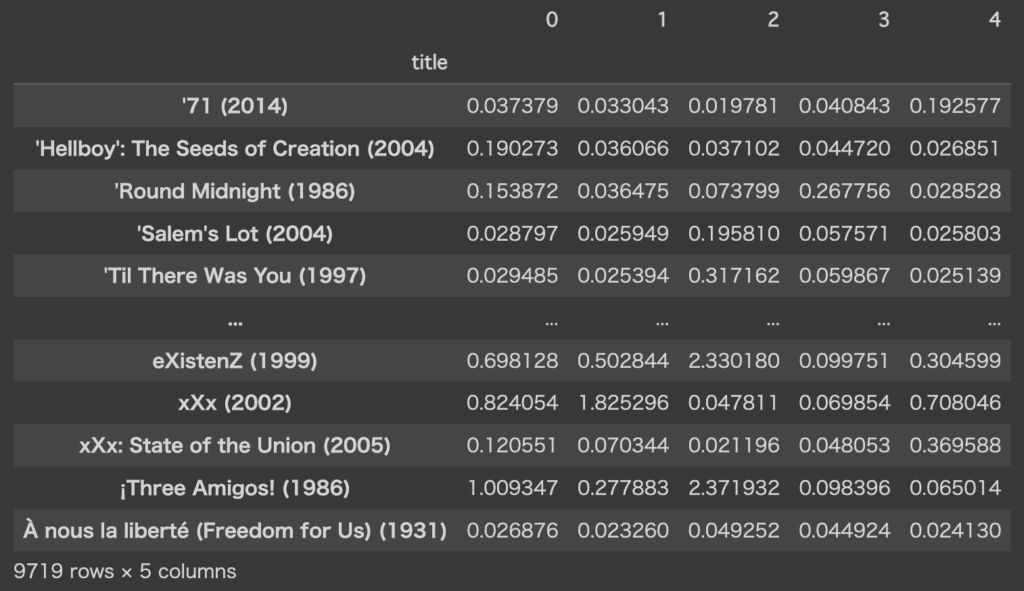
中身を詳しく見てみましょう。第0列目を降順ソートし、値の大きい10行を可視化します。
df_W.sort_values(0, ascending=False).head(10).style.bar(color='green', axis=None)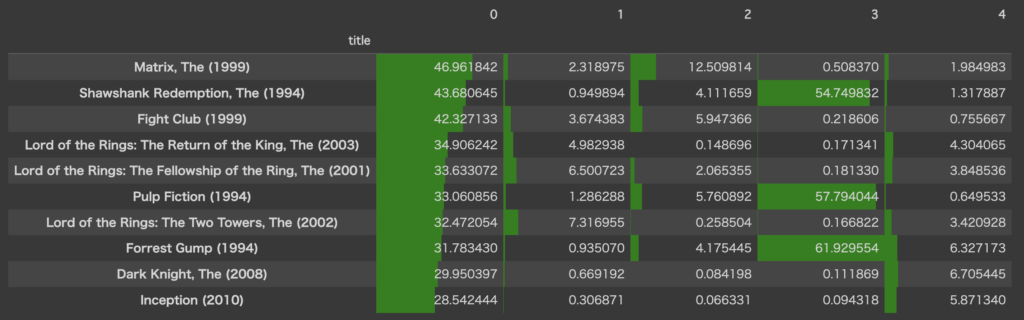
これを見ると、第0列が大きい映画は、どれもタイトルが邦題でなくとも分かるレベルで有名な実写映画が並んでいます。マトリックスやロードオブザリング3部作、ダークナイトがあるので、ざっくり名づけるとすれば”ハリウッド超大作(SF/ファンタジー/アクション)”でしょうか?
また、第3列の値が大きい映画が3タイトルあります(ショーシャンク、パルプフィクション、フォレスト・ガンプ)。偶然かこの3作どれも公開年が1994年となっているので、何かしら共通の要因をもっていそうです。(特定の年代に特に好まれている、とか?)
他の列でも降順ソートし、上から10行をピックアップしてみます。
df_W.sort_values(4, ascending=False).head(10).style.bar(color='green', axis=None)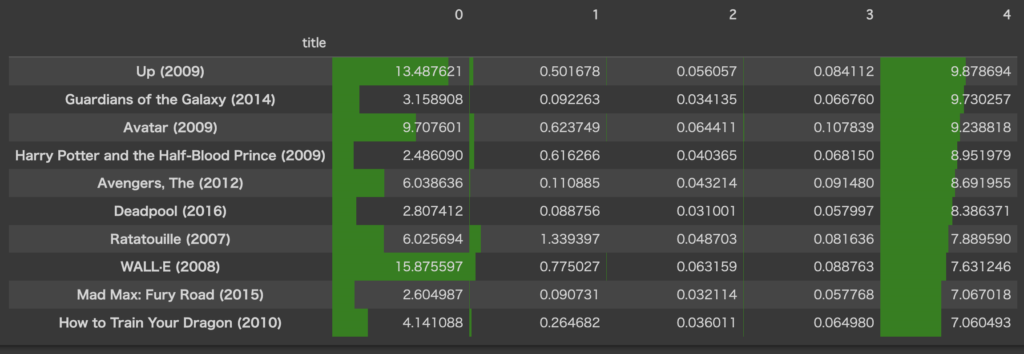
第4列は、Up(=カールじいさんの空飛ぶ家)、アベンジャーズ、ウォーリーなど、比較的子供でも楽しめる作品が上位に来ています。これもざっくり名づけるならば“ディズニー映画”とかですかね?(一応マーベル作品もディズニーに属してるので)
最後に、スターウォーズ関連作品の結果を見てみます。
df_W.filter(like='Star Wars', axis=0).style.bar(color='green', axis=None)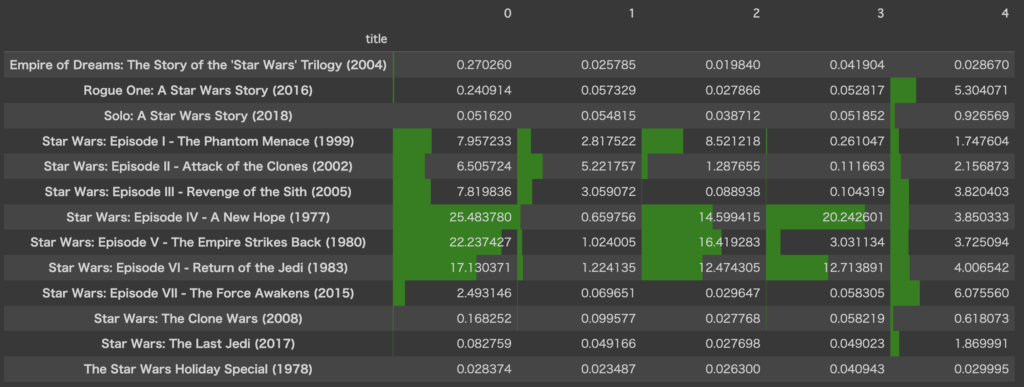
エピソードIV~VIの3部作がかなり特徴的な値となっているので、この3部作の評価は割と似通っているみたいです。I~IIIの3部作も似た値をとっています。
あと、ローグ・ワンとエピソードVIIも近しい値をとっているので、やはり公開年が近い映画はレビューの傾向も近いのかもしれません。
NMFを確率モデルで実行するメリット
先ほど書いた通りNMFはscikit-learnで簡単に実行できるので、「わざわざ確率モデルで実行するメリットはあるのか?」という疑問が浮かぶ方もいらっしゃると思います。
正直なところ、今回実装してみて「別に確率モデルじゃなくてもいいかな…」という感想を持ちました。
というのも、scikit-learn版でも同じデータで実行してみたのですが、変分推論だと10分以上かかる計算がわずか数秒で終わってしまいました。コーディング量や計算量では、scikit-learnに軍配が上がる結果となったのです。$W$の結果も目視でざっと見た限りでは、確率モデル版・sklearn版で大きな違いはなさそうでした。
from sklearn.decomposition import NMF
model_sk = NMF(n_components=5, init='random', random_state=0, max_iter=10000)
W_sk = model_sk.fit_transform(data)
H_sk = model_sk.components_もちろん確率モデルにしかないメリットもあります。例えば、「$K$の値をいくつにすべきか」という問いに対し、いくつかの値で実行してみて、周辺尤度を比較し一番値が良かった設定を採用する、というアプローチが可能になるようです。
ただ、実務では数値上の良し悪しより結果の解釈性に重点が置かれることもあります。例えば、周辺尤度で比べた結果$K=20$がベストとなったとしても、$W$の各20列にどのような特徴があるかをひとつひとつ調べるのは手間ですし、用途によっては列が多すぎて実用性が下がってしまうリスクもあります。
だったら5とか10とかある程度小さい値でいくつかトライし、比較的解釈性の高い$K$を採用する、というフローが現実的なのかなと個人的には思いました。
また、$x_{dn}$にポアソン分布を設定してしまうと整数値しか扱えなくなるのも若干手間だなと感じました。まあこれは指数分布なんかを使えば回避できるのかもしれませんが。
まとめ
本記事では、非負値行列分解(NMF)の解説と確率モデル表現、Pyroでの実行方法についてご紹介しました。
結果として、NMFを確率モデルで行う意義はあまり見えなかったのですが、Pyroの練習ができたのと分析結果がけっこう興味深かったので、個人的には満足。
参考文献
はじめまして。現在、この辺りの分野を学習中の学部3年の者です。
ひとつ質問させていただきたくご連絡いたしました。
XをWとHの積で近似するとき、WとHの事前分布はガンマ分布、事後分布は対数正規分布にして変分推論を実行しておりますが、この2つの分布はどういった経緯(?)で今回仮定したのでしょうか。経験的にこれらを仮定すると結果が上手くいくことをご存知だったりするのでしょうか。
お手数おかけしますが、ご返信いただけますと嬉しい限りです。
よろしくお願いいたします。
コメントありがとうございます。ブログにコメント頂いたの初めてだったので、気づくの遅くなりすみません。。。
→特に経験則など持ってないのですが、まず事前分布にガンマ分布を使った理由は、こちらの書籍にてポアソン分布・ガンマ分布を使用したNMFが取り上げられていたからです。(参考文献として挙げ忘れてました、、、)
近似分布として対数正規分布を使ったのは、ガンマ分布と同様正の値しか取らない点と、パラメータ\muと\sigmaによって分布がどう変わるかが、ガンマ分布より直感的に分かりやすいからです。
ガンマ分布には2つのパラメータがありますが、その2つの大小で平均・分散がどう変わるのかが直感的ではないと(個人的には)思っています。
またパラメータ定義も2種類あり(形状パラメータverと尺度パラメータver)、各ライブラリでどちらが使われているのかいちいち調べるのも面倒なので、今回は対数正規分布を選択しました。
ガンマ分布の定義やパラメータについては、Wikipediaを参照いただくとわかりやすいと思います。
→更新式とは、こちらで紹介されているような、WとHの値を求める際の逐次的な計算式のことでしょうか?であれば今回は発生してないです。
今回は変分推論なので、求めるのはWやHそのものではありません。目的関数の値が収束するような、WやHがしたがう事後分布のパラメータ\mu, \sigmaを求めています。
ですので、\muと\sigmaの更新処理は発生していると言えるかもしれません。
ご期待に沿えているか自信ないですが、ご参考になれば幸いです。
こちらこそ返信遅くなり大変申し訳ないです。
いただいたご返信で分かった気にはなっていますが、ちょっと怪しいので参考文献の方買ってみ他ので、理解を深めようと思います。ありがとうございました。
すいません、追加でもうひとつお伺い致します。
今回、行列WとHの更新処理は発生しない感じでしょうか。