Pyroで混合ベルヌーイによるクラスタリングをやってみる

混合分布モデルでは、離散値の場合は混合ポアソンモデル、連続値の場合は混合ガウスモデルが使われることが多いですが、この2つ以外にも適当な確率分布を使った「混合○○モデル」を定義することはできます。

今回は、データが0 or 1のバイナリーのときに適用できる混合ベルヌーイモデルのご紹介とともに、混合ベルヌーイモデルによるMNISTのクラスタリングをPyroで実装してみます。

混合ベルヌーイモデルについて

Machine Learning: a Probabilistic Perspectiveを参考に説明します。

各データのインデックスを$i$、各データの次元数を$D$とし、各次元は0か1の値をとるとします。また、各データ$x_{i}$は$1\sim K$のどれかのクラスターに所属します。

このとき、データ$x_i$がクラスター$k$($k=1,\dots,K$)に所属している場合、各次元$x_{ij}$の値の取り方を式で表現すると以下になります。

$$
p(x_i|z_i=k, \phi_{jk})=\prod_{j=1}^D Ber(x_{ij}|\phi_{jk})=\prod_{j=1}^D \phi_{jk}^{x_{ij}}(1-\phi_{jk})^{1-x_{ij}}
$$

ただし、$z_i$は各データ$i$が所属するクラスターを表すインデックス、$\phi_{jk}$は$z_i=k$のときに、$j$次元目の値$x_{ij}$が1となる確率とします。

また、データ$i$がクラスター$k$に所属する確率を以下で定義します。

$$
p(z_i=k|\theta)=\theta_k
$$

パラメータ$\phi_{jk}$の事前分布には、ベータ分布$Beta(a,b)$を用います($a,b$はハイパーパラメータ)。

また、各クラスターへの所属確率$\theta=(\theta_{1},\dots,\theta_{K})$は合計1になるので、事前分布にはディリクレ分布$Dir(\alpha)$を使います。
(ちなみに、もし$K=2$の場合は、ディリクレ分布はベータ分布と同一となります)

この混合ベルヌーイモデルを使うことで以下が分かります。

• $z_i$の事後分布を見ることで、データ$i$がどのクラスタリングに所属するかを判定できる
• $\phi_{jk}$の事後分布をみることで、クラスター$k$は$1\sim D$のどの次元が1になりやすいか/なりにくいかが分かる

MNISTで実装してみる

MNISTにこの混合ベルヌーイを適用してみます。

MNISTは各セルに0~255の値が入っているのですが、これが128未満なら0、128以上なら1になるように変換します。

また、今回は0~9の中でも、比較的形状が異なる2,3,4の3つの数字だけを使用します。
(混合ベルヌーイのようなシンプルなモデルで 0~9の数字をうまくクラスタリングするのはさすがに難しい…)

最初の15個だけ見てみるとこんな感じ。

実装にはPPLの一種であるPyroを用いて、変分ベイズで各パラメータの事後分布(厳密には事後分布の近似分布)を求めます。

実行環境はGoogle colaboratoryです。「ランタイム」→「ランタイムのタイプを変更」→ハードウェア アクセラレータをGPUに設定しておきます。

まずはPyroをインストール。

!pip install pyro-ppl

必要なライブラリをインポート。

from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch.distributions import constraints
from torch.distributions.dirichlet import Dirichlet
from torch.distributions.beta import Beta
from torch.distributions.categorical import Categorical
from torch.distributions.bernoulli import Bernoulli

from tqdm.notebook import tqdm

import pyro
from pyro import poutine
import pyro.distributions as dist
from pyro.infer import SVI, TraceEnum_ELBO, config_enumerate, infer_discrete
import pyro.optim
from pyro.ops.indexing import Vindex

torch.set_default_tensor_type(torch.cuda.FloatTensor)

PytorchのデバイスをGPUに設定します。

device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

MNISTデータを読み込みます。『ゼロから作るディープラーニング』のコードのmnist.pyを使ってpickleファイルに保存済みです。

同じmnist.pyのload_mnist関数を使って読み込みます。

train, test = load_mnist(normalize=False, flatten=False, one_hot_label=False)

0~255の数字を128で割り、四捨五入することで0 or 1に変換します。
また先述の理由で2,3,4の3つに絞ります。

data = train[0]
data = np.trunc(data / 128)
cluster = train[1]

target_idx = np.where((cluster  > 1) & (cluster < 5))

data_filter = np.squeeze(data[target_idx]).copy()
cluster_filter = cluster[target_idx]

データをTensorに変換、データ数や次元数を変数に格納します。

x = torch.tensor(data_filter.reshape(data_filter.shape[0], -1).copy()).int()

K = 3 # クラスター数
N = x.size(0) # データ数
L = x.size(1) # 次元数

print(f'nrow : {N}')
# nrow : 17931
print(f'ncol : {L}')
# ncol : 784

続いて、今回用いる混合ベルヌーイモデルを定義します。

@config_enumerate
def model(N, obs, L, K):
    # theta: 各クラスターへの所属確率
    theta = pyro.sample("theta", dist.Dirichlet(torch.ones(K)))
    
    with pyro.plate("cluster_param_plate", K):
        # phi: 各次元が1をとる確率(クラスターによって異なる)
        phi = pyro.sample("phi", dist.Dirichlet(torch.ones(L, 2)).to_event(1))

    with pyro.plate("data_plate", N):
        # z: データiが所属するクラスターのインデックス
        z = pyro.sample("z", dist.Categorical(theta))
        # x: 各次元の0 or 1の値
        x = pyro.sample("x", dist.Categorical(phi[z]).to_event(1), obs=obs)

    return z, x

先ほど$\theta$の事前分布にはベータ分布を用いると書きましたが、コード上はディリクレ分布を使用しています(2次元なので実質同じ)。
ディリクレ分布のハイパーパラメータ$\alpha$の要素はすべて1に設定しています。

to_event()の中の数字は何にしないといけないのか、そもそもいつ設定しないといけないのかは、正直理解しきれていないためエラーが出なければOKとしてます...。

次に、モデルの近似分布を定義します。

関心のあるパラメータ$\theta$と$\phi$は、どちらも合計1になるので、ディリクレ分布で近似します。
つまり、モデルに一番フィットする$Dir(\alpha)$の$\alpha$や$Dir(\beta)$の$\beta$を求めるのが今回の目的です。

def guide(N, obs, L, K):
    # thetaの事後分布の近似分布
    alpha_q = pyro.param('alpha', init_tensor=torch.ones(K), constraint=constraints.positive)
    pyro.sample('theta', dist.Dirichlet(alpha_q))
    
    # phiの事後分布の近似分布
    beta_q = pyro.param('beta', torch.ones(K, L, 2), constraint=constraints.positive)
    with pyro.plate("cluster_param_plate", K):
        pyro.sample('phi', dist.Dirichlet(beta_q).to_event(1))

では、パラメータの最適化計算を回します。最適化手法はAdamを利用します。
(正直ここもどれがいいのかよくわかっていません...公式ドキュメントのTips通りにしています)

pyro.clear_param_store()

# Adamの設定
adam_params = {"lr": 0.001, "betas": (0.9, 0.9)}
optimizer = pyro.optim.Adam(adam_params)
elbo = TraceEnum_ELBO(max_plate_nesting=1)

pyro.set_rng_seed(123)
svi = SVI(model, guide, optimizer, loss=elbo)

print('initial loss = '.format(svi.loss(model, guide, N, x, L, K)))

gradient_norms = defaultdict(list)
for name, value in pyro.get_param_store().named_parameters():
    value.register_hook(lambda g, name=name: gradient_norms[name].append(g.norm().item()))

losses = []
for _ in tqdm(range(10000)):
    loss = svi.step(N, x, L, K)
    losses.append(loss)

# lossの推移を可視化
plt.figure(figsize=(10, 3)).set_facecolor('white')
plt.plot(losses)
plt.xlabel('iters')
plt.ylabel('loss')
plt.yscale('log')
plt.title('Convergence  of SVI')
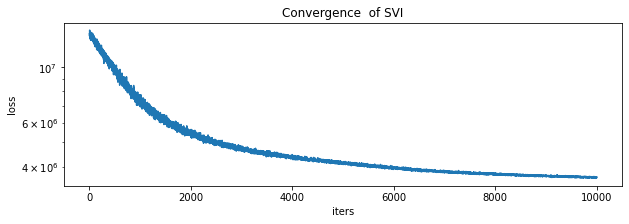
plt.show()

実際のlossの推移が以下です。私の環境では計算時間は13分ほどでした。

では、最適化したパラメータ$\alpha$と$\beta$の中身を見てみます。

for name in pyro.get_param_store():
    print("{}: {}".format(name, pyro.param(name)))

alpha: tensor([5.5001, 4.9932, 5.3846], grad_fn=)
beta: tensor([[[34.5352,  0.0637],
         [34.4314,  0.0639],
         [33.3835,  0.0708],
         ...,
         [34.3279,  0.0646],
         [34.3799,  0.0678],
         [33.8727,  0.0606]],

        [[35.8078,  0.0689],
         [35.6468,  0.0666],
         [33.5353,  0.0670],
         ...,
         [32.7626,  0.0685],
         [35.2914,  0.0647],
         [36.8544,  0.0699]],

        [[33.3329,  0.0667],
         [34.5523,  0.0660],
         [35.3043,  0.0633],
         ...,
         [32.6343,  0.0643],
         [34.5878,  0.0655],
         [34.5712,  0.0659]]], grad_fn=)

まずalphaは、3要素とも似た値が入っていますが、これは2,3,4の数の比率が大体同じであることを意味しています。
実際、2,3,4どれも約6,000個データがあり、サンプルサイズの偏りはほとんどないです。

betaのほうは値の大きさが偏っています。これは、ほとんどのセルは基本0が入っている(0をとる確率が大きい)ことを表しています。

次に、各データがどのクラスターに所属したのかを求めます。

guide_trace = poutine.trace(guide).get_trace(N, x, L, K)
trained_model = poutine.replay(model, trace=guide_trace)

def classifier(temperature=0):
    inferred_model = infer_discrete(trained_model, temperature=temperature,
                                    first_available_dim=-2)
    trace = poutine.trace(inferred_model).get_trace(N, x, L, K)
    return trace.nodes["z"]["value"]

pyro.set_rng_seed(123)
pred_cluster = classifier()

# 各クラスターのサンプルサイズをカウント
print(pred_cluster.unique(return_counts=True))

# (tensor([0, 1, 2]), tensor([6331, 5481, 6119]))

やはり各クラスターはサンプルサイズがそこまで偏ってはいなさそうですね。
ただし、クラスター0~2のどれが実際のクラスター(2,3,4)のどれに対応するかは、これだけではわかりません。

そこで、結果を可視化してみます。
扱いやすくするため、tensor形式からnumpy配列に変換します。

# 予測クラスター
pred_cluster_np = pred_cluster.to('cpu').detach().numpy().copy()

# beta
beta_np = pyro.param("beta").to('cpu').detach().numpy().copy()

このbeta_npをもとに、各セルの取る値の事後期待値を、クラスター別に計算します。
ディリクレ分布の期待値の式は以下。

$$
E[x_{ij}|z_i=k] = \frac{\beta_{jk}^1}{\beta_{jk}^0 + \beta_{jk}^1}
$$

theta_pred = (beta_np[:, :, 1] / np.sum(beta_np, axis=2)).reshape(3, 28, 28)

そして、このセル別期待値をクラスターごとに可視化します。

fig, axes = plt.subplots(1, 3, figsize=(10, 5))
for k, ax in enumerate(axes.flatten()):
    ax.imshow(theta_pred[k])
fig.show()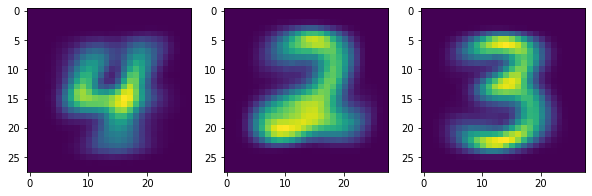

これを見ると、クラスター0が4、クラスター1が2、クラスター2が3に対応していることが分かります。うまく分けられていますね。
もちろん、今回は0~9の中でも簡単な数字だけ選んだのでうまくいっているのですが...。

いつ役に立つの？

じゃあこの混合ベルヌーイがいつ役立つのかというと、カテゴリカルデータを使ったクラスタリングに利用できます。

例えば、「あなたは～ですか？」に対して「はい」「いいえ」という2択の回答が得られているアンケート調査があれば、それをもとにモニターを似た回答者同士にまとめることが出来るんですね。

これが2択でなく「1～5で選んでください」みたいな5択の場合、混合ベルヌーイでなく混合カテゴリカルモデルを使えばいいです。
ベルヌーイ分布をカテゴリカル分布に変えるだけです。(詳しい説明は余力がないので省略します)

Pyroについてはあんまりネットに日本語の情報が転がっていないので、実装するのはなかなか大変なのですが、みなさんもぜひ機会があれば試してみてください。
(ミス等あれば、ぜひコメントにてご指摘いただけるとありがたいです)