マーケティング施策の効果測定の手法で最もメジャーなもののひとつに、マーケティングミックスモデル (MMM) があります。特に近年では、3rd Party Cookieの規制や、Google等の企業がオープンソースとしてMMMのライブラリを公開してくれていたりと、よりその利用シーンが増えてきているのかなと思います。
- Robyn (Meta)
- LightweightMMM, Meridian (Google)
- PyMC-Marketing (PyMC)
MMMでは予測よりも、目的変数(売上やKPI)に対するマーケティング施策の影響の解釈に重きを置かれるため、基本的には線形モデルのようなホワイトボックスな手法が用いられます。そんな中、Googleが新たに提案したニューラルネットワークを用いたマーケティングミックスモデリングについて、本記事ではご紹介します。
NNNの元論文はこちら (HTML版もあり)
NNNとは?
NNNは、従来のMMMのような線形モデルではなく、ニューラルネットワークを基盤とした新しいマーケティングミックスモデリングの手法です。名前の由来は、『Next-Generation Neural Networks for Marketing Mix Modeling』の頭文字らしいです。
(MMMに合わせて、無理やり”NNN”にしている感は否めない)
従来のMMMと比較したNNNの利点として、以下の要素を加味できる点です。特に3と4の要素が、MMMとの大きな違いとなります。
- 長期的な広告残存効果(adstock)
- 広告間の複雑な相互作用の影響
- 広告変数と目的変数の間に存在する中間変数
- 広告の量(出稿量・金額)だけでなく、各広告クリエイティブの違い
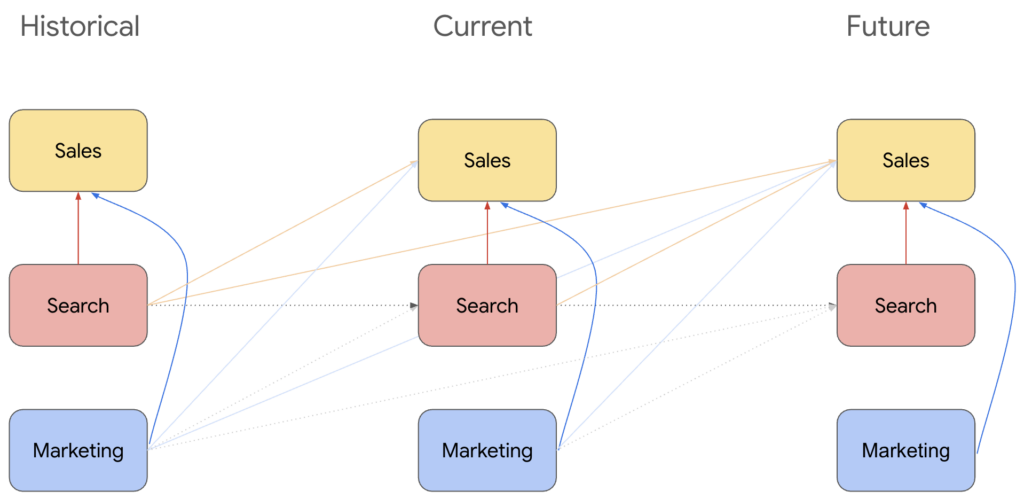
3については、以下のNNNにおける変数間の構造を示した図(元論文から引用)を見てもらうとイメージつくかなと思います。
- マーケティング施策 (
Marketing)- 目的変数である売上 (
Sales) に影響を与える - 中間変数である検索 (
Search) へも影響を与える - 同時期だけでなく、将来の値へも継続的に影響する
- 目的変数である売上 (
- 中間変数 (
Search)- こちらもマーケティング施策と同様、売上 (
Sales)への影響がある - 同時期だけでなく、将来の売上への継続的な影響を仮定しているのも同じ
- こちらもマーケティング施策と同様、売上 (
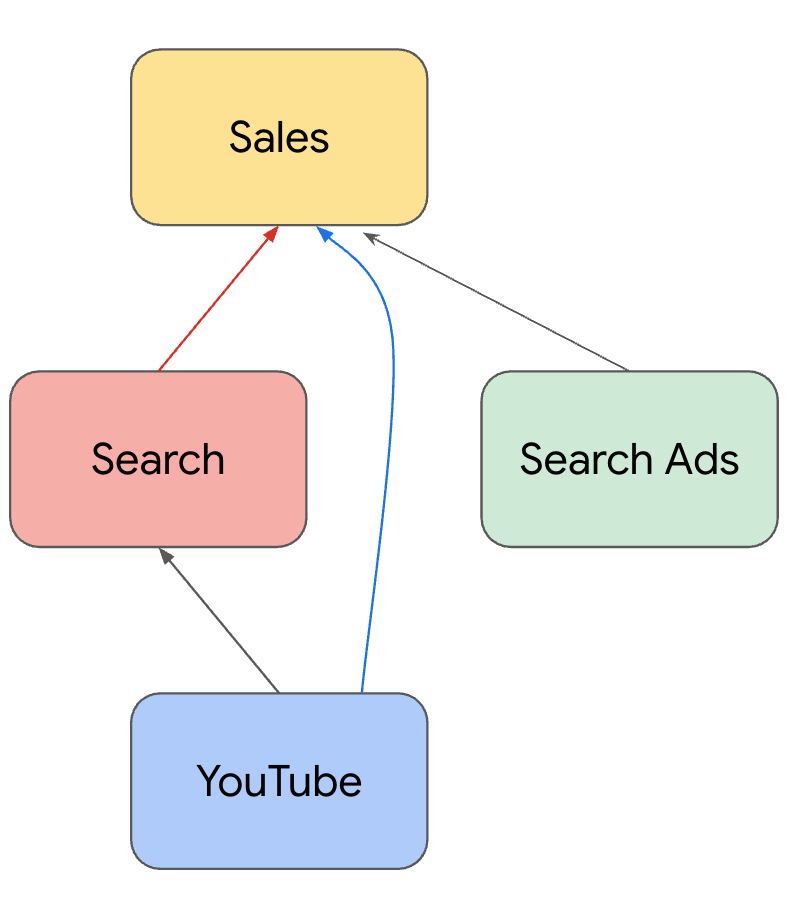
4について、従来のMMMでは、広告変数として出稿金額や出稿量など、いわゆるスカラーを使用します。しかしこれでは、広告クリエイティブの違いを加味することができません。例えば、素材が異なる2つTVCMの出稿したとしても、スカラーではその違いをモデルに反映することが困難です。
一方NNNでは、動画をベクトルに変換する埋め込みモデルを使い、各クリエイティブをベクトル化することで、クリエイティブの違いをモデルに反映しています。また検索についても、検索クエリを言語埋め込みモデルによってベクトル化することで、検索クエリの違いも加味しています。
要するに、量だけでなく質の違いも捉えようとしている、ということです。
ちなみにこの論文では、中間変数として基本的にGoogle検索のみを前提としています。その根拠として、インフルエンザの発生率や自動車販売の予測に、Google検索のクエリ埋め込みの使用が非常に有効であるという過去研究があるようです。また、Google検索の量は季節や曜日ごとに異なるため、そのデータを使うことでモデルに季節性を反映することができる、とも主張しています。
(執筆者がGoogleの人間っていう理由も当然あるとは思います)
また広告チャネルについても、論文中の説明や実験では、検索広告とYouTube広告のみを用いています。これは単純にGoogleが得られるデータだからという理由だと思います。当然TVCMのような他の広告チャネルも利用可能なはずです。
(街頭広告のようなOOHであれば、画像埋め込みモデルを使用すればOK?)
NNNで使用するデータの構造
NNNでは、インプットデータとしてランク4のテンソル$X$を使用します。このテンソルの形状は$(G, T, C, D)$となり、それぞれ以下のように定義されます。
- $G$:エリアの数 (例. 都道府県ごとに分析する場合、$G=47$)
- $T$:総時点数 (例. 週次データが全部で52週間ある場合、$T = 52$)
- $C$: 全てのチャネルの総数
- 広告チャネルだけでなく、中間変数(Google検索)や目的変数(売上)も含む
- $D$:全チャネルにわたる埋め込み次元の最大サイズ
- 売上などスカラーにしかなり得ないデータや、埋め込み次元が$D$未満の場合は、$D$次元になるよう0で埋める
- 埋め込みには既存の学習済みモデルを使用
以下では、$X$の各要素について詳細を見ていきます。
検索クエリの埋め込み
まずは検索クエリの埋め込みです。検索語$s$を、事前学習済みのエンコーダーによって512次元の埋め込み$e(s)$に変換します。この処理を複数の$s$に対して実行し、それらを足し合わせることで、検索埋め込み$X_{g,t,\text{Search}}$が次のように生成されます。
$$
X_{g,t,\text{Search}}=\sum_{s\in S_{g,t}}e(s)
$$
ここで、$S_{g,t}$はエリア$g$、期間$t$における検索クエリの集合を表します。また$e$はエンコーダーを表します。
検索広告の埋め込み
まず前提として、検索広告として使用するデータには、次の2つの選択肢が存在します。
- その検索広告が表示されたときに、ユーザーが検索していた用語
- その検索広告自体に使用されているコピー素材
この論文では上記1のデータを使用し、先ほどの検索クエリと同様の変換を実施して埋め込み$X_{g,t,\text{SearchAds},:}$を作成します。
(広告インプレッション数も何かしらの方法で組み込んでいるようですが、詳細は記載されていませんでした)
YouTube広告の埋め込み
YouTube広告においても、先ほどの検索広告のように以下の2つの選択肢があります。
- YouTube広告が表示されたときに、ユーザーが視聴していた動画コンテンツ
- YouTube広告自体のコンテンツ
こちらは検索広告と異なり、上記の2のデータを使用し、事前学習済みの動画埋め込みモデルによって埋め込みに変換し、$X_{g,t,\text{YouTube},:}$を作成します。
(動画視聴数も加味しているようだが、こちらも詳細不明)
NNNのモデルアーキテクチャ
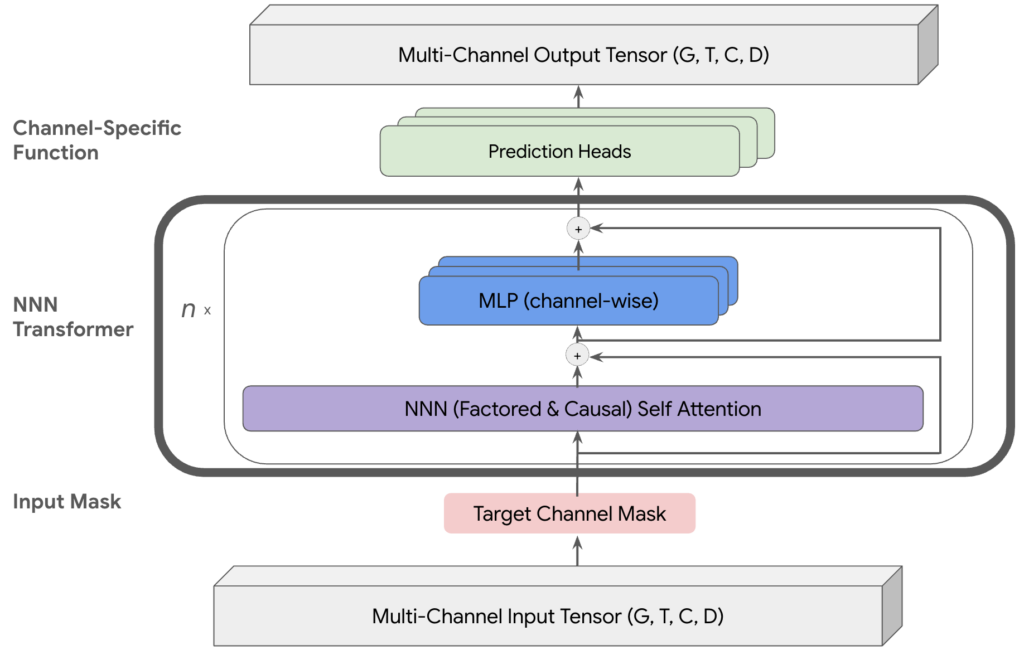
NNNのモデルアーキテクチャの全体像は以下のようになっています(元論文より引用)。以下で各要素の詳細を見ていきます。
Transformer
形状$(G, T, C, D)$の入力テンソル$X$は、目的変数に該当する箇所をマスキングされた後、NNN Transformerを$N$回通過します。Transformerの各レイヤーは、次のように表現できます:
$$
X^{(n)}:=\text{Transformer}(X^{(n-1)},\Theta)
$$
ここで、$X^{(0)} := X$は入力データであり、$\Theta$はモデルのパラメータの集合です。
このTransformaerの中には、さらに2つの要素(Self AttentionとMLP)が存在します。NNNにおいて重要なのは、前者のAttention機構です。広告間の相互作用や、長期adstockをモデルに反映させるために、この機構に工夫が加えられています。(Factored Self Attention)
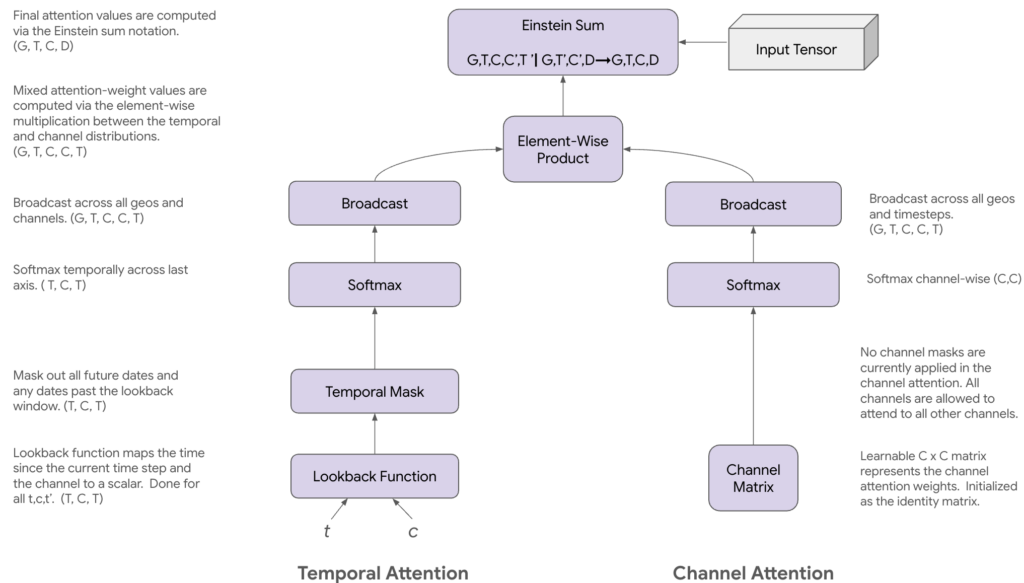
Temporal Attention
Factored Self Attentionは、さらに2つの要素で成り立っています。そのうちの1つが、Temporal Attentionです。このAttention機構では、2つの時刻$t$と$t^\prime$の間の関係性を表現する関数$a_\text{time}$を学習します。つまりは、広告効果の残存や減衰についての構造を学習することを目指します。
具体的な手順としては、入力テンソル$X \in \mathbb{R}^{G \times T \times C \times D}$に対し、まず以下の2つの値を作成します。
- 正規化された時間差:$\Delta_{t,t^{\prime}}=(t-t^{\prime})/\omega \in \mathbb{R}$
- ターゲットチャネル$c$を表すワンホットエンコーディング:$E_{c} \in \mathbb{R}^{C}$
ここで、$\omega$はルックバックウインドウサイズと言い、$t$と$t^\prime$の間がどれくらい近ければ、関係性が存在することを許容するかをコントロールします。
関数$a_{\text{time}}:\mathbb{R}^{1+C}\rightarrow\mathbb{R}$として、ReLU活性化関数と128の隠れユニットを持つ単一隠れ層の多層パーセプトロン (MLP) を用います。この関数で以下のAttentionスコア$s_{t,t^{\prime},c}$を定義します。
$$
s_{t,t^{\prime},c} = a_{\text{time}}(\text{concat}(\Delta_{t,t^{\prime}},E_{c}))
$$
このスコアを要素として持つテンソル$S_{\text{raw}} \in \mathbb{R}^{T \times T \times C}$を作成した後、時間的な因果関係が現実的な値となるよう、加法的なマスク$M \in \{0, -\infty\}^{T \times T}$を適用します。
$$
M_{t,t^{\prime}}=
\begin{cases}
0 & \text{if } t-\omega<t^{\prime}\leq t \\
-\infty & \text{otherwise}
\end{cases}
$$
これはつまり、
- 時刻$t^\prime$が$t$より先の時刻
- $t$よりも前のタイミングすぎる(時刻の差が$\omega$以上ある)
のどちらかに該当する場合は、$-\infty$を足し、2時点間の関係性が存在しないという構造を盛り込んでいます。
さらに言い換えると、時刻$t$の売上や検索量は、$t$より将来に打つ広告や、$t$よりはるか昔のタイミングで打った広告の影響を受けない、という至極当たり前の構造をモデルに反映してます。
このマスキングを$S_{\text{raw}}$(をエリア$G$方向にブロードキャスティングし転置したもの)に適用し、スコア$S^\prime\in\mathbb{R}^{G \times T \times C \times T}$を計算します。
$$
(S^\prime)_{g,t,c,t^\prime} = (\text{transpose}(S_\text{raw}))_{g,t,c,t^\prime} + M_{t,t^\prime}
$$
最終的なAttentionの重み$W_{\text{time}} \in \mathbb{R}^{G \times T \times C \times T}$は、$(S^{\prime})_{g,t,c,:}$を$\tau$でスケーリングした後、時間次元$t^{\prime}$にわたるソフトマックス変換によって得られます。
$$
(W_\text{time})_{g,t,c,t^\prime}=\text{softmax}_{t^{\prime}}\left(\frac{(S^{\prime})_{g,t,c,:}}{\tau}\right)_{t^{\prime}}
$$
Channel Attention
Factored Self Attentionの2つ目の要素として、チャネル間の相互作用を捉えるためのメカニズムであるChannel Attentionも存在します。こちらは先述のTemporal Attentionよりも単純で、チャネル相互作用行列$\psi\in\mathbb{R}^{C \times C}$を定義し、その行列をソフトマックス変換($\tau$によるスケーリングつき)したものを、重み$W_{\text{chan}} \in \mathbb{R}^{G \times T \times C \times C}$とします。
$$
(W_{\text{chan}})_{g,t,c,c^{\prime}}=\text{softmax}_{c^{\prime}}\left(\frac{\psi_{c,:}}{\tau}\right)_{c^{\prime}}
$$
このChannel Attentionのポイントとしては、学習の際の$\psi$の初期値として、単位行列を指定することにあります。これは、「チャネル$c$に最も影響のあるチャネルは、$c$自身である」という知見を反映させるためのテクニックのようです。
ちなみにこの重み$W_{\text{chan}}$も、時間・エリア方向にブロードキャスティングする必要があるのですが、そのすべて一律で同じとしています。
これら2つのAttentionの重みを、適切なブロードキャスティングの後、要素ごとに乗算することで、最終的なAttentionの重み$W_\text{fac}\in\mathbb{R}^{G \times T \times C \times C \times T}$を算出します。
$$
(W_\text{fac})_{g, t, c, c’, t’} = (W_\text{time})_{g, t, c, t’} \cdot (W_\text{chan})_{g, t, c, c’}
$$
このテンソル$(W_\text{fac})_{g, t, c, c’, t’}$は、$(g, t, c)$と$(g, t’, c’)$の間の関係性を表現しています。
最終的な出力$O\in\mathbb{R}^{G \times T \times C \times D}$は、この重みを使用して入力テンソル$X$と掛け合わせることによって計算されます。
$$
O_{g, t, c, d} = \sum_{t’=0}^{T-1}\sum_{c^\prime\in \mathcal{C}} (W_\text{fac})_{g, t, c, c’, t’} \cdot X_{g, t’, c’, d}
$$
売上と検索の予測
先ほどのTransformerを適用した後、売上$\hat{\text{Sales}}_{g,t}$の予測値を算出します。まず、Transformerを$N$回適用した中間表現$X^{(N)}_{g,t,c}$を正規化します。
$$
\hat{X}_{g,t,c}^{(N)} = \frac{X_{g,t,c}^{(N)}}{||X_{g,t,c}^{(N)}||}
$$
この$\hat{X}_{g,t,c}^{(N)}$と、エリアを表現するワンホットエンコーディング$g$を、パラメータ$\theta^{c}$を持つMLP ResNetの$P$に入力します。このMLP ResNetは、最終層に1つの隠れユニットとシグモイド活性化関数を持たせます。そして、各チャネル$c$のボリューム$V_{g,t,c}$(検索なら検索数、広告なら出稿数や出稿金額など?)を掛け合わせることで、売上予測を計算します。
$$
\hat{\text{Sales}}_{g,t} = F(X)_{g,t,\text{sales},0} := \sum_{c} V_{g,t,c}\cdot P(X_{g,t,c}^{(N)}, g, \theta^{c})
$$
またNNNでは、売上だけでなく検索値を予測する構造も定義可能です。一部のチャネルに関するTransformerの結果をMLP Resnetに投入し、検索予測値$\hat{\text{Search}}_{t,g}$が生成されます。
$$
\hat{\text{Search}}_{t,g}=F(X)_{g,t,\text{Search},:}
:=\text{MLPResnet}\left(
\text{concat}\left([X^{(n)}_{g,t,c}\mid c\in C^{\prime}]
\right)
\right)
$$
ここで、$C^{\prime}$は予測に使用するチャネルの集合を表します。論文中では$C^\prime = \{\text{YouTube}, \text{Search}\}$としています。「Searchの予測モデルの特長量にSearch自身を入れていいの?」と思ったのですが、よくよく読んでみると、この$\hat{\text{Search}}_{t,g}$は$X_{g,t+1,\text{search},d}$の予測値として定義しているようです。つまり、現在までの検索に関する値を特長量として、1個先の時点の検索値を予測する機構を想定しているようでした。
また$X_{g,t+1,\text{search},d}$の予測値としていることからも、$\hat{\text{Search}}_{t,g}$は実際に検索された数ではなく、エリア$g$, 時点$t$における全検索クエリを埋め込み処理&合計した後の値の予測値であることがわかります。
ちなみにYouTubeや検索広告などの他のチャネルは、予測値を算出する必要がないため定義していません。というのも、これら広告の値は企業がコントロールできるため、そもそも予測する必要がないからです。
損失関数と学習
NNNの学習では、売上予測における損失$L^{\text{sales}}(X,\Theta)$と、検索予測における損失$L^{\text{Search}}(X,\Theta)$の両方を考慮します。これらは、それぞれ平均二乗誤差 (MSE) 損失として定義されます。
$$
L(X) := \alpha \cdot L^\text{sales}(X, \Theta) + (1-\alpha) \cdot L^\text{Search}(X,\Theta) + \lambda \cdot \sum_{\theta\in\Theta}|\theta|
$$
ここで、
- $L^{\text{sales}}(X,\Theta) := \frac{1}{G\cdot T} \sum_{g,t} (X_{g,t,\text{sales},0} – \hat{\text{Sales}}_{g,t})^{2}$
- $L^{\text{Search}}(X,\Theta) := \frac{1}{G\cdot(T-1)\cdot D} \sum_{g,t,d} (X_{g,t+1,\text{search},d}-\hat{\text{Search}}_{g,t,d})^{2}$
であり、$\Theta$はモデルが持つ全パラメータ、$\alpha$と$\lambda$はハイパーパラメータとなります。
損失関数に$\lambda$を用いたL1正則化項を用いることで、データのスパース性に対処しているんだと思います。
広告貢献量の測定
学習したモデルを使い、各チャネル$c$の売上に対する効果を推定します。論文では、2つの推定方法が紹介されています。
1. 従来の方法
1つ目は、元データにおける売上予測値と、チャネル$c$の量を0にした場合の売上予測値との差を用いる方法です。
$$
\text{Attribution}_c=\sum_{g,t} \left( \hat{\text{Sales}}(X)_{g,t}−\hat{\text{Sales}}(\tilde{X}^c)_{g,t} \right)
$$
ここで、$X$は元のデータ、${\tilde{X}}^{c}$は$X$におけるチャネル$c$の値を0にしたテンソルです。つまり、チャネル$c$の広告を一切出さなかった場合の売上を反実仮想的に算出し、広告ありの売上値がその反実仮想値をどれくらい上回っているかで広告効果を測定します。この測定方法は、NNNに限らず既存のMMM手法でも適用されることがあるかなと思います。
2. 自己回帰展開
例えばYouTube広告の効果を算出する場合、従来の方法だと、YouTubeの広告量だけを0にし、検索や検索広告に関する値は元データと同じ値を使用します。が、YouTube→検索の影響を加味したモデルを使っているにもかかわらず、YouTubeの値を0にし検索の値は何も変えないというのは、モデルの仮定に反する処理を行っていることになります。
そこで、YouTube→検索の影響も加味した貢献量を推定する方法を考えます。まず以下のように、時刻$P$までのデータを使って予測した一期先予測値$Y_{P+1}$を定義します。
$$
Y_{P+1} := F(X_{\dots,:P,\dots}, \Theta)
$$
さらに、$t=P+K+1$までの予測値を、以下のように逐次的に算出していきます。
$$
Y_{P+1+K} := F(\text{concat}([X_{\dots,:P,\dots},Y^\prime_{P+1},\dots,Y^\prime_{P+K}]), \Theta)
$$
ここで、
$$
Y_t^\prime = \text{concat}[Y_{:,t,\text{sales},:},Y_{:,t,\text{search},:},X_{:,t,c^\prime,:} | \forall c^\prime \notin \{\text{sales, search}\}]
$$
であり、売上と検索にはモデルによる予測値を、それ以外のチャネルは実際の値を用いたテンソルとなります。イメージとしては以下の図が分かりやすいです。
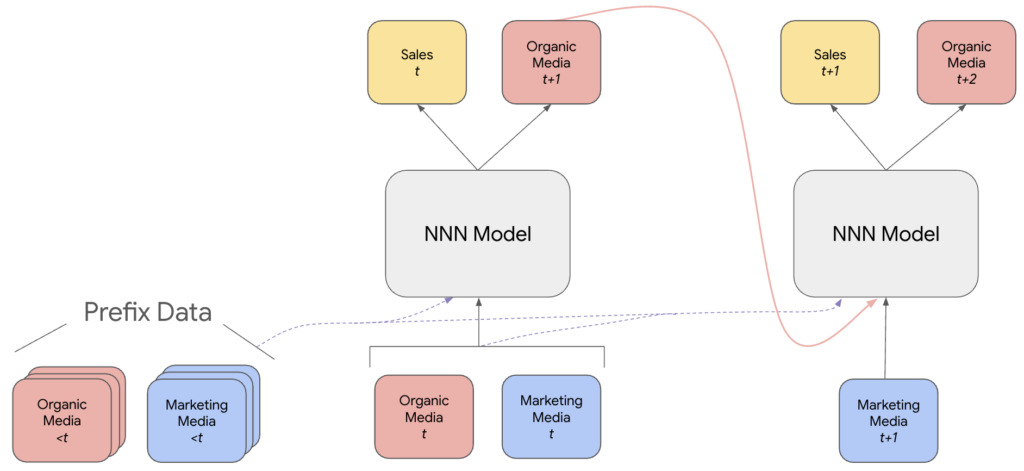
上記と同様の操作により、チャネル$c$の値を0にしたバージョンの予測値$Y_{P+1},\dots,Y_{P+K+1}$も算出し、『1. 従来の方法』と同様に差をとることで、チャネル$c$の効果量を算出します。
この方法をとることで、例えばYouTube広告の効果測定では、『1. 従来の方法』では加味できていなかった検索経由の効果(YouTube広告→検索→売上)も加味した効果量を推定できる、としています。
上記1と2の違いを、シミュレーションデータを用いて比較したのが以下の図です。途中の20週間にYouTube広告を停止した場合の売上予測値の比較を行っています。
- 青:YouTube動画を停止しなかった場合の売上予測値
- オレンジ:YouTube動画を停止した場合の売上予測値 (検索値は元データのまま)
- 赤:YouTube動画を停止した場合の売上予測値 (検索値も予測値を使用)
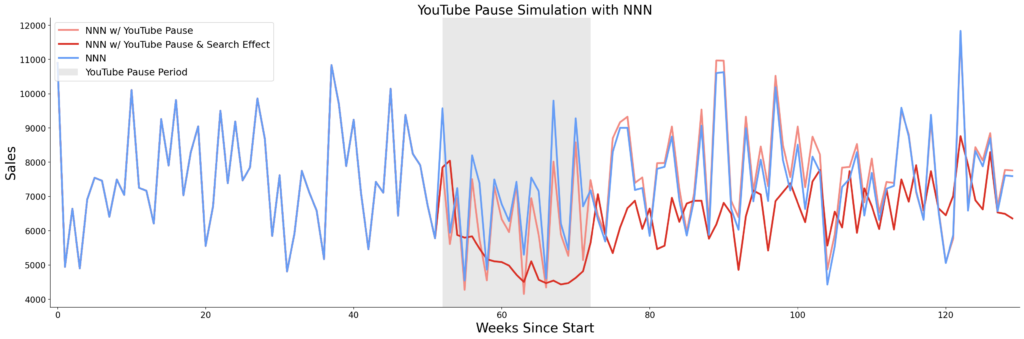
 これを見ると、オレンジ線ではあまり売上に影響が見られませんが、赤線だと「YouTube広告の停止は検索数にも影響を与え、検索数減少により売上が長期的に低下する」という現象を捉えられていることが分かります。
これを見ると、オレンジ線ではあまり売上に影響が見られませんが、赤線だと「YouTube広告の停止は検索数にも影響を与え、検索数減少により売上が長期的に低下する」という現象を捉えられていることが分かります。
もちろん上記はあくまでシミュレーションデータにおける結果なので、現実のデータでここまで明確に違いが生じるとは限りません。が、『2. 自己回帰展開』の方法だと、広告量を変化させたときに、売上だけでなく中間指標もどれくらいの値になるかをシミュレーション可能なのはメリットだなと感じました。
NNNでできないこと・難しいこと
論文中では、MMM(特にベイジアンMMM)と比較してNNNではできないこととして、以下が挙げられていました。
- すべてのパラメータに点推定値を用いるので、モデルの不確実性を表現できない
- 分析者のドメイン知識を盛り込むのが難しい
- モデルアーキテクチャや初期値指定により、ある程度は可能である
それ以外に、論文では特に言及されていないようでしたが、個人的には以下も難しいのかなと感じました
- 売上に影響の大きい広告クリエイティブが分かったとしても、具体的にそのクリエイティブのどの要素が効いているかを特定するのは無理そう
- 既存のMMMの課題(内生性の問題、厳密な効果推定は難しい、等)は、NNNでも依然解決できない
まとめ
本記事では、ニューラルネットワークを用いたMMMの新しい手法であるNNNを紹介しました。個人的に一番おもしろいと思ったのは、広告クリエイティブの違いをモデルに盛り込めるという点です。現状だと難しいかもしれませんが、売上を最大化する広告素材を作り出すことも将来的には可能だったりするのかなーと期待が持てました。
余談ですが、元論文のAppendixにNNNの疑似Pythonコードが載っていたので、シミュレーションデータを使った実装例も本記事に載せようと考えていました。が、埋め込みを作るための元データとなる、検索クエリデータや動画広告データの作成や取得が無理だっため、実装は諦めました。。。
Meridianみたいに、Googleさんがオープンソースとしてコードやシミュレーションデータを公開してくれないかなぁ。
参考文献